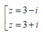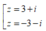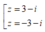Đặt \(\sqrt{8+6i}=x+yi\) với \(x;y\in R\)
\(\Rightarrow8+6i=x^2+2xyi+y^2i^2=x^2-y^2+2xyi\)
\(\Rightarrow\left\{{}\begin{matrix}x^2-y^2=8\\xy=3\end{matrix}\right.\) \(\Rightarrow x^2-\dfrac{9}{x^2}=8\)
\(\Rightarrow x^4-8x^2-9=0\Rightarrow\left[{}\begin{matrix}x=3\Rightarrow y=1\\x=-3\Rightarrow y=-1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\sqrt{8+6i}=3+i\\\sqrt{8+6i}=-3-i\end{matrix}\right.\)
Đúng 0
Bình luận (0)
