Question

tìm các cạnh và các góc của tam giác ABC biết AB =21cm góc B=42 độ góc C=56 độ

Answer 1

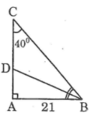
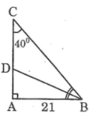
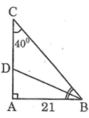
Xét ΔABC có \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)

=>\(\widehat{A}=180^0-42^0-56^0=82^0\)

Xét ΔABC có \(\dfrac{BC}{sinA}=\dfrac{AC}{sinB}=\dfrac{AB}{sinC}\)

=>\(\dfrac{21}{sin56}=\dfrac{BC}{sin82}=\dfrac{AC}{sin42}\)

=>\(BC\simeq25,08\left(cm\right);AC\simeq16,95\left(cm\right)\)

Answer 2

\(\widehat{A}=180^o-42^o-56^o=82^o\)

Ta có:

\(\dfrac{AC}{sinB}=\dfrac{AB}{sinC}=\dfrac{BC}{sinA}\)\(\Leftrightarrow\left\{{}\begin{matrix}AC=\dfrac{21.sin42}{sin56}\simeq16,95cm\\BC=\dfrac{21.sin82}{sin56}\simeq25,1cm\end{matrix}\right.\)