Các câu hỏi tương tự
Cho hình chữ nhật ABCD với AD=3AB lấy M là trên BC, đường thẳng AM cắt đường thẳng CD tại P, đường thẳng EF\(\perp\)AM cắt AB tại E, CD tại F, đường phân giác của ∠DAM cắt CD tại K.
a) C/M: EF=DK+3BM
b) C/M: \(\dfrac{1}{AB^2}=\dfrac{1}{AM^2}+\dfrac{9}{AP^2}\)Cho hình thoi ABCD. Lấy điểm E trên cạnh AB sao cho \(\dfrac{AE}{AB}=\dfrac{2}{3}\) và điểm F trên cạnh CD sao cho \(\dfrac{DF}{DC}=\dfrac{1}{3}\)
a) Tứ giác AECF, EBFD là hình gì?
b) AD và EF kéo dài gặp nhau ở H. Tính \(\dfrac{HD}{HA}\)
c) Chứng minh HC vuông góc với AC và F là trọng tâm tam giác HDB
Cho hình thang ABCD (AB // CD) có hai đường chéo cắt nhau tại O. Đường thẳng qua O song song với hai đáy cắt hai cạnh bên tại E và F.
a, Tìm độ dài các cạnh đáy của hình thang biết OC : OA = 1 : 3 và độ dài của đường trung bình là 24cm.
b, C/minh: OE = OF
c, C/minh hệ thức : \(\dfrac{1}{AB}+\dfrac{1}{CD}=\dfrac{2}{EF}\)
Cho hình thang ABCD (AB // CD, AB < CD). Gọi P; Q lần lượt là trung điểm của AB và CD. C/minh: \(PQ< \dfrac{AD+BC}{2}\)
Cho tứ giác ABCD.Gọi E,F,K theo thứ tự là trung điểm của AD,BC,AC
A) So sánh độ dài EK và CD, KF và AB
B) Chứng minh rằng: EF≤\(\dfrac{AB+BC}{2}\)
biết tỉ số giữa hai đoạn thẳng AB và CD bằng \(\dfrac{3}{7}\), CD=14cm. độ dài đoạn thẳng AB là:
Viết tỉ số của hai đoạn thẳng có độ dài như sau:
a) AB = 5cm và CD = 15 cm
b) EF = 48cm và GH = 16dm
c) PQ = 1,2m và MN = 24cm
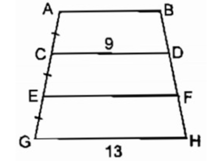
Trên hình bs.1, ta có AB // CD // EF // GH và AC CE EG. Biết CD 9, GH 13. Các độ dài AB và EF bằng:A. 8 và 10B.6 và 12C. 7 và 11D. 7 và 12 Hãy chọn phương án đúng
Đọc tiếp
Trên hình bs.1, ta có AB // CD // EF // GH và AC = CE = EG. Biết CD = 9, GH = 13. Các độ dài AB và EF bằng:
A. 8 và 10
B.6 và 12
C. 7 và 11
D. 7 và 12
Hãy chọn phương án đúng













