
giải gấp giúp mình với ạ
```text
Bài 3. Cho biểu thức: \( A = \frac{x}{x-2} - \frac{2x+1}{x+2} - \frac{x^2+8}{4-x^2} \) \((x \neq 2; x \neq -2)\); \( B = \frac{5}{x+1} \) \((x \neq -1)\)
a) Rút gọn A.
b) Tính giá trị của A biết \( x = -6 \).
c) Tìm x để \( A = 2 \).
d) Tìm giá trị nguyên của x để \( M = A : B \) nhận giá trị nguyên lớn nhất.
```
a: \(A=\dfrac{x}{x-2}-\dfrac{2x+1}{x+2}-\dfrac{x^2+8}{4-x^2}\)
\(=\dfrac{x}{x-2}-\dfrac{2x+1}{x+2}+\dfrac{x^2+8}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{x\left(x+2\right)-\left(2x+1\right)\left(x-2\right)+x^2+8}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{x^2+2x-\left(2x^2-4x+x-2\right)+x^2+8}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{2x^2+2x+8-2x^2+3x+2}{\left(x-2\right)\left(x+2\right)}=\dfrac{5x+10}{\left(x-2\right)\left(x+2\right)}=\dfrac{5}{x-2}\)
b: Khi x=-6 thì \(A=\dfrac{5}{-6-2}=\dfrac{5}{-8}=\dfrac{-5}{8}\)
c: A=2
=>\(\dfrac{5}{x-2}=2\)
=>\(x-2=\dfrac{5}{2}\)
=>\(x=\dfrac{5}{2}+2=\dfrac{9}{2}\left(nhận\right)\)
d: \(M=A:B=\dfrac{5}{x-2}:\dfrac{5}{x+1}=\dfrac{x+1}{x-2}\)
\(=\dfrac{x-2+3}{x-2}=1+\dfrac{3}{x-2}\)
Để M là số nguyên lớn nhất thì x-2=1
=>x=3
\(\dfrac{x}{x-2}-\dfrac{2x+1}{x+2}-\dfrac{x^2+8}{4-x^2}\\ =\dfrac{x}{x-2}-\dfrac{2x+1}{x+2}+\dfrac{x^2+8}{(x-2)(x+2)}\\ =\dfrac{x(x+2)-(2x+1)(x-2)+x^2+8}{(x-2)(x+2)}\\ =\dfrac{5x+10}{(x-2)(x+2)}=\dfrac{5(x+2)}{(x-2)(x+2)}=\dfrac{5}{x-2}\)
b; thay x = -6 vào A ta được:
\(\dfrac{5}{-6-2}=-\dfrac{5}{8}\)
c; để A = 2 thì \(\dfrac{5}{x-2}=2⇒\:x=4,5\)
d; \(M=A:B=\dfrac{5}{x-2}:\dfrac{5}{x+1}\)
\(=\dfrac{5}{x-2}\cdot\dfrac{x+1}{5}=\dfrac{x+1}{x-2}=\dfrac{x-2+3}{x-2}=1+\dfrac{3}{x-2}\)
để M đạt giá trị nguyên lớn nhất thì x - 2 = 1 ⇒ x = 3









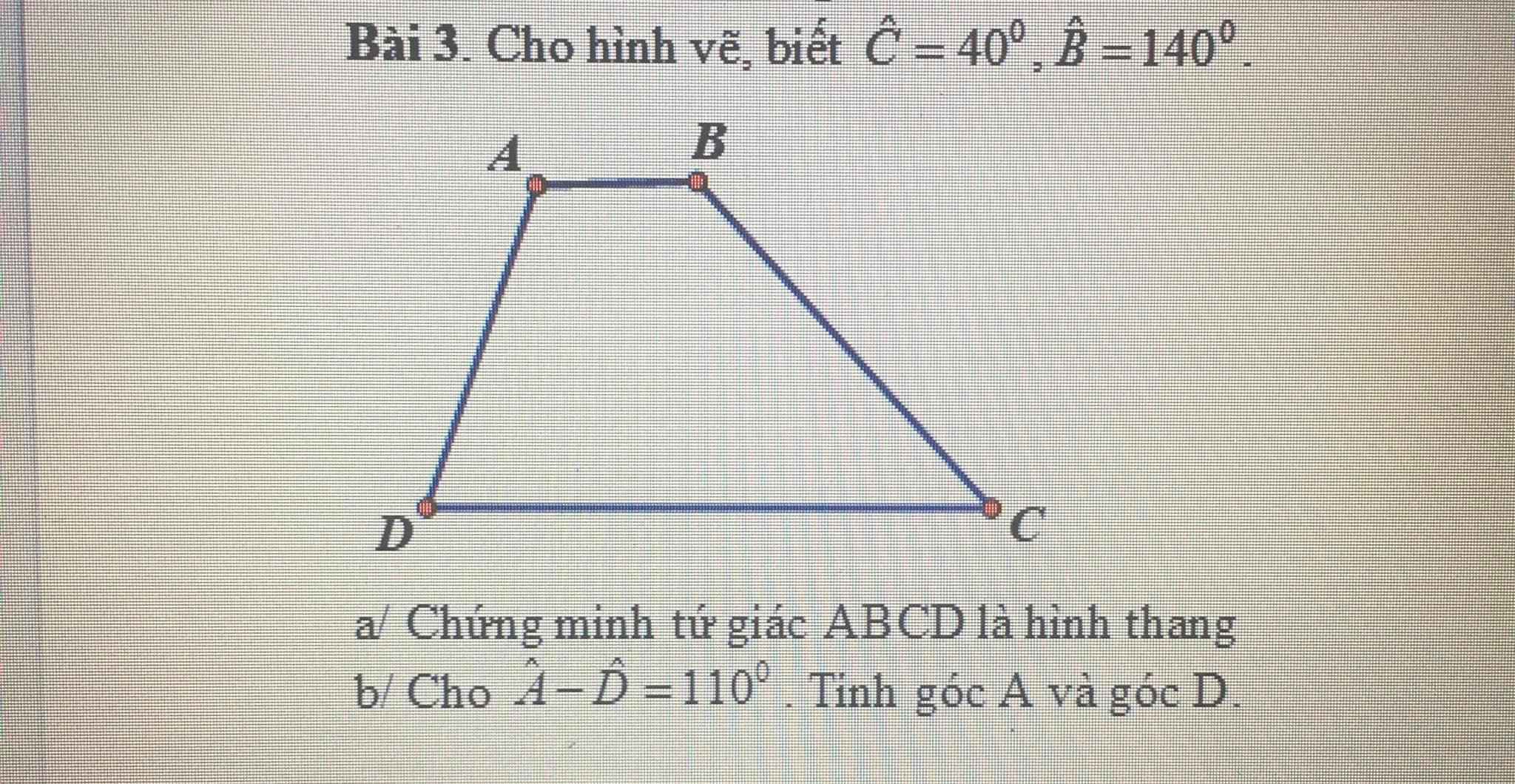

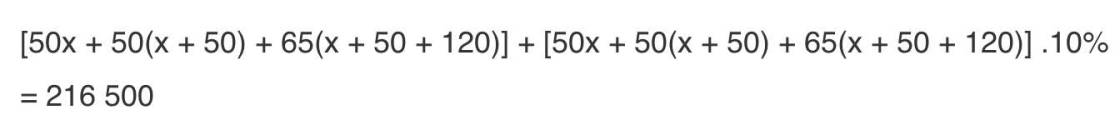




 Vẽ hình và giải chi tiết giúp mình với, đang cần gấp cảm ơn nhiều ạ
Vẽ hình và giải chi tiết giúp mình với, đang cần gấp cảm ơn nhiều ạ



