Các câu hỏi tương tự
Cho hàm số f thỏa mãn
f
cot
x
sin
2
x
+
cos
2
x
,
∀
x
∈
0
;
π
. Giá trị lớn nhất của hàm số
g
x
f
sin
2
x
.
f...
Đọc tiếp
Cho hàm số f thỏa mãn f cot x = sin 2 x + cos 2 x , ∀ x ∈ 0 ; π . Giá trị lớn nhất của hàm số g x = f sin 2 x . f cos 2 x trên ℝ là
A. 6 125 .
B. 1 20 .
C. 19 500 .
D. 1 25 .
Cho hàm số y f (x) liên tục trên
ℝ
và có đồ thị như hình vẽ bên.Tập hợp tất cả các giá trị thực của tham số m để phương trình f (sinx) m có nghiệm thuộc khoảng (0;
π
) là A. [-1;3) B. (-1;1) C. (-1;3) D. [-1;1 )
Đọc tiếp
Cho hàm số y = f (x) liên tục trên ℝ và có đồ thị như hình vẽ bên.
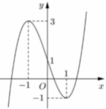
Tập hợp tất cả các giá trị thực của tham số m để phương trình f (sinx) = m có nghiệm thuộc khoảng (0; π ) là
A. [-1;3)
B. (-1;1)
C. (-1;3)
D. [-1;1 )
Cho hàm số yf(x) liên tục trên
ℝ
và có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của tham số m để phương trình
f
f
sin
x
m
có nghiệm thuộc khoảng
0
;
π
? A. 2 B. 3 C. 4 D. 5
Đọc tiếp
Cho hàm số y=f(x) liên tục trên ℝ và có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của tham số m để phương trình f f sin x = m có nghiệm thuộc khoảng 0 ; π ?
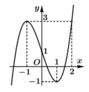
A. 2
B. 3
C. 4
D. 5
Cho hàm số
y
f
x
liên tục trên
ℝ
và có đồ thị như hình vẽ. Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để phương trình
f
sin
x
3
sin
x
+
m
có nghiệm thuộc khoảng
0
;
π
. Tổng các phần tử của S bằng A. -10 B. -8 C. -...
Đọc tiếp
Cho hàm số y = f x liên tục trên ℝ và có đồ thị như hình vẽ. Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để phương trình f sin x = 3 sin x + m có nghiệm thuộc khoảng 0 ; π . Tổng các phần tử của S bằng
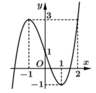
A. -10
B. -8
C. -6
D. -5
Cho hàm số
y
f
x
xác định và liên tục trên
ℝ
0
thỏa mãn:
x
2
f
2
x
+
2
x
−
1
f
x
x
.
f
x
−
1
với...
Đọc tiếp
Cho hàm số y = f x xác định và liên tục trên ℝ \ 0 thỏa mãn: x 2 f 2 x + 2 x − 1 f x = x . f ' x − 1 với ∀ x ∈ ℝ \ 0 đồng thời f 1 = − 2. Tính ∫ 1 2 f x d x
A. − ln 2 2 − 1
B. − ln 2 − 1 2
C. − ln 2 − 3 2
D. − ln 2 2 − 3 2
Cho hàm số y f(x) xác định trên
ℝ
và có đạo hàm f (x) thỏa mãn
f
x
1
-
x
x
+
2
.
g
x
+
2018
trong đó
g
x
0
,
∀
x
∈
ℝ
. Hàm số
y...
Đọc tiếp
Cho hàm số y = f(x) xác định trên ℝ và có đạo hàm f '(x) thỏa mãn f ' x = 1 - x x + 2 . g x + 2018 trong đó g x < 0 , ∀ x ∈ ℝ . Hàm số y = f 1 - x + 2018 x + 2019 nghịch biến trên khoảng nào?
A. 1 ; + ∞
B. 0 ; 3
C. - ∞ ; 3
D. 3 ; + ∞
Cho hàm số y f(x) xác định và liên tục trên
ℝ
thỏa mãn đồng thời các điều kiện sau: f(x) 0 với
∀
x
∈
ℝ
,
f
(
x
)
-
e
x
.
f
2
x
với
∀
x
∈
ℝ
f
0
1
2...
Đọc tiếp
Cho hàm số y = f(x) xác định và liên tục trên ℝ thỏa mãn đồng thời các điều kiện sau: f(x) > 0 với ∀ x ∈ ℝ , f ' ( x ) = - e x . f 2 x với ∀ x ∈ ℝ f 0 = 1 2 . Phương trình tiếp tuyến của đồ thị tại điểm có hoành độ x 0 = ln 2 là:
A. 2 x + 9 y - 2 ln 2 = 0
B. 2 x - 9 y - 2 ln 2 + 3 = 0
C. 2 x - 9 y + 2 ln 2 - 3 = 0
D. 2 x + 9 y - 2 ln 2 - 3 = 0
Cho hàm f có tập xác định là
K
⊂
ℝ
, đồng thời f có đạo hàm f(x) trên K . Xét hai phát biểu sau:(1) Nếu
f
x
0
≠
0
thì
x
0
không là điểm cực trị của hàm f trên K.(2) Nếu qua
x
0
mà f(x) có sự đổi dấu thì
x
0
là điểm cực trị của hàm f.Chọn khẳng định đúng. A...
Đọc tiếp
Cho hàm f có tập xác định là K ⊂ ℝ , đồng thời f có đạo hàm f'(x) trên K . Xét hai phát biểu sau:
(1) Nếu f ' x 0 ≠ 0 thì x 0 không là điểm cực trị của hàm f trên K.
(2) Nếu qua x 0 mà f'(x) có sự đổi dấu thì x 0 là điểm cực trị của hàm f.
Chọn khẳng định đúng.
A. (1), (2) đều đúng.
B. (1),(2) đều sai.
C. (1) sai, (2) đúng.
D. (1) đúng, (2) sai
Tìm tập xác định
D
ℝ
của hàm số
y
log
2
x
+
1
-
1
A.
D
(
-
∞
;
1
]
B.
D
3
;
+
∞...
Đọc tiếp
Tìm tập xác định D = ℝ của hàm số y = log 2 x + 1 - 1
A. D = ( - ∞ ; 1 ]
B. D = 3 ; + ∞
C. D = [ 1 ; + ∞ )
D. D = ℝ \ 3
Cho hàm số
y
a
x
4
+
b
x
2
+
c
a
≠
0
,
a
,
b
,
c
∈
ℝ
có đồ thị như hình bên. Xác định dấu của a, b, c. A. a0, b0, c0 B. a0, b0, c0...
Đọc tiếp
Cho hàm số y = a x 4 + b x 2 + c a ≠ 0 , a , b , c ∈ ℝ có đồ thị như hình bên. Xác định dấu của a, b, c.
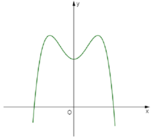
A. a<0, b>0, c>0
B. a>0, b>0, c>0
C. a<0, b>0, c<0
D. a>0, b<0, c>0