Đáp án B
Phương pháp: Điểm biểu diễn của số phức z = a +bi, (a,b ∈ R) là M (a;b)
Cách giải: Số phức z = –4 + 3i được biểu diễn bởi điểm M có tọa độ M (–4;3)
Đáp án B
Phương pháp: Điểm biểu diễn của số phức z = a +bi, (a,b ∈ R) là M (a;b)
Cách giải: Số phức z = –4 + 3i được biểu diễn bởi điểm M có tọa độ M (–4;3)
Trên mặt phẳng tọa độ, số phức z = 3i - 4 được biểu diễn bởi điểm A, B, C, D?
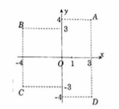
A. Điểm D
B. Điểm B
C. Điểm A
D. Điểm C
Cho số phức z thỏa mãn: z 1 + 2 i - z ¯ 2 - 3 i = - 4 + 12 i . Tìm tọa độ điểm M biểu diễn số phức z.
A. M 3 ; 1
B. M 3 ; - 1
C. M - 1 ; 3
D. M 1 ; 3
Cho số phức z= a+bi (a,b∈R). Biết tập hợp các điểm A biểu diễn hình học số phức z là đường tròn (C) có tâm I(4;3) và bán kính R=3. Đặt M là giá trị lớn nhất, m là giá trị nhỏ nhất của F=4a+3b-1. Tính giá trị M+ m.
A. M+ m=63
B. M+ m=48
C. M+ m=50
D. M+ m=41
Cho số phức z và số phức liên hợp của nó z có điểm biểu diễn là M, M’. Số phức z . ( 4 + 3 i ) và số phức liên hợp của nó có điểm biểu diễn lần lượt là N, N’. Biết rằng 4 điểm M, N, M’, N’ tạo thành hình chữ nhật. Tìm giá trị nhỏ nhất của biểu thức | z + 4 i - 5 | .
A. 1 2
B. 2 5
C. 5 34
D. 4 13
Cho số phức z thỏa mãn phương trình 3 + 2 i z + z - i 2 = 4 + i . Tìm tọa độ điểm M biểu diễn số phức z.
A. M - 1 ; 1
B. M - 1 ; - 1
C. M 1 ; 1
D. M 1 ; - 1
Cho số phức z thỏa mãn (2 - i)z = (2 + i)(1 - 3i). Gọi M là điểm biểu diễn của z. Khi đó tọa độ điểm M là.
A. M(3;1)
B. M(3;-1)
C. M(1;3)
D. M(1;-3)
Cho số thực a thay đổi và số phức z thỏa mãn z a 2 + 1 = i - a 1 - a a - 2 i . Trên mặt phẳng tọa độ, gọi M là điểm biểu diễn số phức z . Khoảng cách giữa hai điểm M và I (-3; 4) (khi a thay đổi) là:
A. 4
B. 3
C. 5
D. 6
Cho số phức z = 3 + 5 i có điểm biểu diễn trên mặt phẳng tọa độ là M. Tìm tọa độ điểm M
A. M 3 ; − 5 .
B. M − 3 ; − 5 .
C. M 3 ; 5 .
D. M 5 ; 3 .
Tập hợp các điểm M trên mặt phẳng tọa độ biểu diễn các số phức z thỏa mãn điều kiện z + z + 3 = 4 là
A. Đường thẳng x = 1 2
B. Đường thẳng x = - 7 2
C. Hai đường thẳng x = 1 2 và x = 7 2
D. Hai đường thẳng x = 1 2 và x = - 7 2