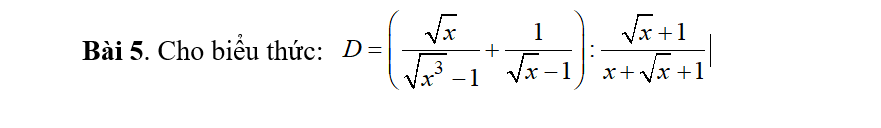5) \(...=\dfrac{\left(\sqrt{a}+2\right)^2}{\sqrt{a}+2}-\dfrac{\left(\sqrt{a}+2\right)\left(\sqrt{a}-2\right)}{\sqrt{a}-2}\)
\(=\sqrt{a}+2-\left(\sqrt{a}+2\right)=0\)
6) \(...=\dfrac{\left(\sqrt{a}+\sqrt{b}\right)^2}{\sqrt{a}+\sqrt{b}}-\dfrac{\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}-\sqrt{b}\right)}{\sqrt{a}+\sqrt{b}}\)
\(=\sqrt{a}+\sqrt{b}-\left(\sqrt{a}-\sqrt{b}\right)=2\sqrt{b}\)
7) \(...=\left(\dfrac{1-\left(\sqrt{a}\right)^3}{1-\sqrt{a}}+\sqrt{a}\right)\left[\dfrac{1-\sqrt{a}}{\left(1-\sqrt{a}\right)\left(1+\sqrt{a}\right)}\right]^2\)
\(=\left[\dfrac{\left(1-\sqrt{a}\right)\left(1+\sqrt{a}+a\right)}{1-\sqrt{a}}+\sqrt{a}\right]\left(\dfrac{1}{1+\sqrt{a}}\right)^2\)
\(=\left(1+\sqrt{a}+a+\sqrt{a}\right)\dfrac{1}{\left(1+\sqrt{a}\right)^2}\)
\(=\dfrac{1+2\sqrt{a}+a}{1+2\sqrt{a}+a}=1\)