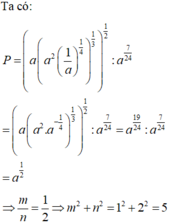Các câu hỏi tương tự
Rút gọn biểu thức
A
a
5
3
.
a
7
3
a
4
.
a
−
2
7...
Đọc tiếp
Rút gọn biểu thức A = a 5 3 . a 7 3 a 4 . a − 2 7 với a > 0 ta được kết quả A = a m n , trong đó m , n ∈ ℕ * và m n là phân số tối giản. Khẳng định nào sau đây đúng?
A. m 2 + n 2 = 43
B. 2 m 2 + n = 15
C. m 2 − n 2 = 25
D. 3 m 2 − 2 n = 2
Rút gọn biểu thức
A
a
5
3
.
a
7
3
a
4
.
a
−
2
7...
Đọc tiếp
Rút gọn biểu thức A = a 5 3 . a 7 3 a 4 . a − 2 7 với a > 0 ta được kết quả A = a m n trong đó m , n ∈ ℕ ∗ và m n là phân số tối giản. Khẳng định nào sau đây đúng ?
A. m 2 − n 2 = 25
B. m 2 − n 2 = 43
C. 3 m 2 − 2 n = 2
D. 2 m 2 + n = 15
Câu 1 : Cho biểu thức :
A= a^3+2a^2-1/ a^3+2a^2+2a+1
a/ Rút gọn biểu thức
B/ CMR nếu a là số nguyên âm thì giá trị biểu thức tìm đc của câu a là 1 phân số tối giản
Biết
a
b
(trong đó
a
b
là phân số tối giản và
a
,
b
∈
ℕ
*
)
là giá trị của tham số thực m để cho hàm số
y
2
3
x
3
−
m
x
2
−
2
3
m
2
−
1...
Đọc tiếp
Biết a b (trong đó a b là phân số tối giản và a , b ∈ ℕ * ) là giá trị của tham số thực m để cho hàm số y = 2 3 x 3 − m x 2 − 2 3 m 2 − 1 x + 2 3 có hai điểm cực trị x 1 , x 2 sao cho x 1 x 2 + 2 x 1 + x 2 = 1. Tính giá trị biểu thức S = a 2 + b 2 .
A. S = 13
B. S = 25
C. S = 10
D. S = 34
Biết
a
b
(trong đó
a
b
là phân số tối giản và
a
,
b
∈
ℕ
*
) là giá trị của tham số m thực để cho hàm số
y
2
3
x
3
−
m
x
2
−
2
3
m
2...
Đọc tiếp
Biết a b (trong đó a b là phân số tối giản và a , b ∈ ℕ * ) là giá trị của tham số m thực để cho hàm số y = 2 3 x 3 − m x 2 − 2 3 m 2 − 1 x + 2 3 có hai điểm cực trị x 1 , x 2 sao cho x 1 x 2 + 2 x 1 + x 2 = 1 . Tính giá trị biểu thức S = a 2 + b 2
A. S= 13
B. S = 25
C. S = 10
D. S = 34
\(A=\frac{a^3+2a^2-1}{a^3+2a^2+2a+1}\)
a/ Rút gọn biểu thức
b/ CMR nếu a là nguyên âm thì giá trị của biểu thức tìm đc câu a là 1 phân số tối giản
Gọi a, b là hai giá trị thực để hàm số
f
x
2
x
2
+
6
3
−
a...
Đọc tiếp
Gọi a, b là hai giá trị thực để hàm số f x = 2 x 2 + 6 3 − a x x 2 − 1 , x ≠ 1 a + b x + 2 , x = 1 liên tục tại x = 1. Biết rằng b = m n ; m ∈ ℤ , n ∈ ℕ và m n là phân số tối giản. Tính P = m + 2n
A. P = -17
B. P = =-5
C. P = -23
D. P = -13
Biết
a
b
(trong đó
a
b
là phân số tối giản, a,b∈
N
*
) là giá trị thực của tham số m để hàm số
y
2
x
3
-
3
mx
2
-
6
(
3
m...
Đọc tiếp
Biết a b (trong đó a b là phân số tối giản, a,b∈ N * ) là giá trị thực của tham số m để hàm số y = 2 x 3 - 3 mx 2 - 6 ( 3 m 2 - 1 ) x + 2018 có hai điểm cực trị x1;x2 thỏa mãn x 1 x 2 + 2 ( x 1 + x 2 ) = 1 . Tính P= a+2b.
A. P=5.
B. P=6.
C. P=7.
D. P=8.
Cho hàm số
f
x
3
x
−
4
+
x
+
1
.2
7
−
x
−
6
x
+
3
. Giả sử
m
0
a
b
(...
Đọc tiếp
Cho hàm số f x = 3 x − 4 + x + 1 .2 7 − x − 6 x + 3 . Giả sử m 0 = a b ( a , b ∈ ℤ , a b là phân số tối giản) là giá trị nhỏ nhất của tham số thực m sao cho phương trình f 7 − 4 6 x − 9 x 2 + 2 m − 1 = 0 có số nghiệm nhiều nhất. Tính giá trị của biểu thức P = a + b 2
A. P = -1
B. P = 7
C. P = 11
D. P = 9