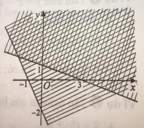
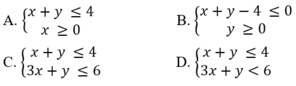Phương trình đường thẳng \(\left(a\right):y=ax+b\)
mà \(a=tan\alpha=-\dfrac{1}{2}\) (vì \(\alpha\) quay ngược chiều kim đồng hồ)
\(\Rightarrow y=-\dfrac{1}{2}x+b\)
\(\left(0;2\right)\in\left(a\right)\Leftrightarrow2=-\dfrac{1}{2}.0+b\Leftrightarrow b=2\)
\(\Rightarrow\left(a\right):y=-\dfrac{1}{2}x+2\)
\(\Leftrightarrow\left(a\right):x+2y=2\)
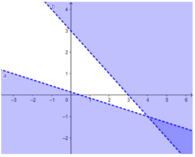
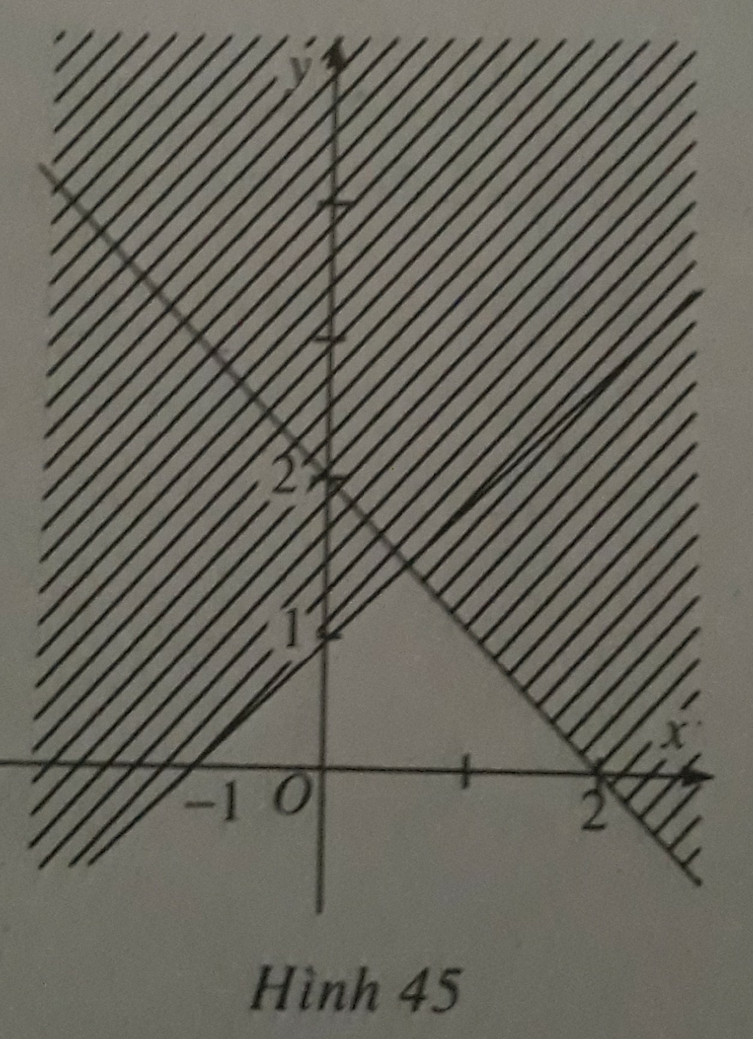
Đây là miền nghiệm của \(x+2y\ge2\)
Đây là miền nghiệm \(x+2y\le2\)
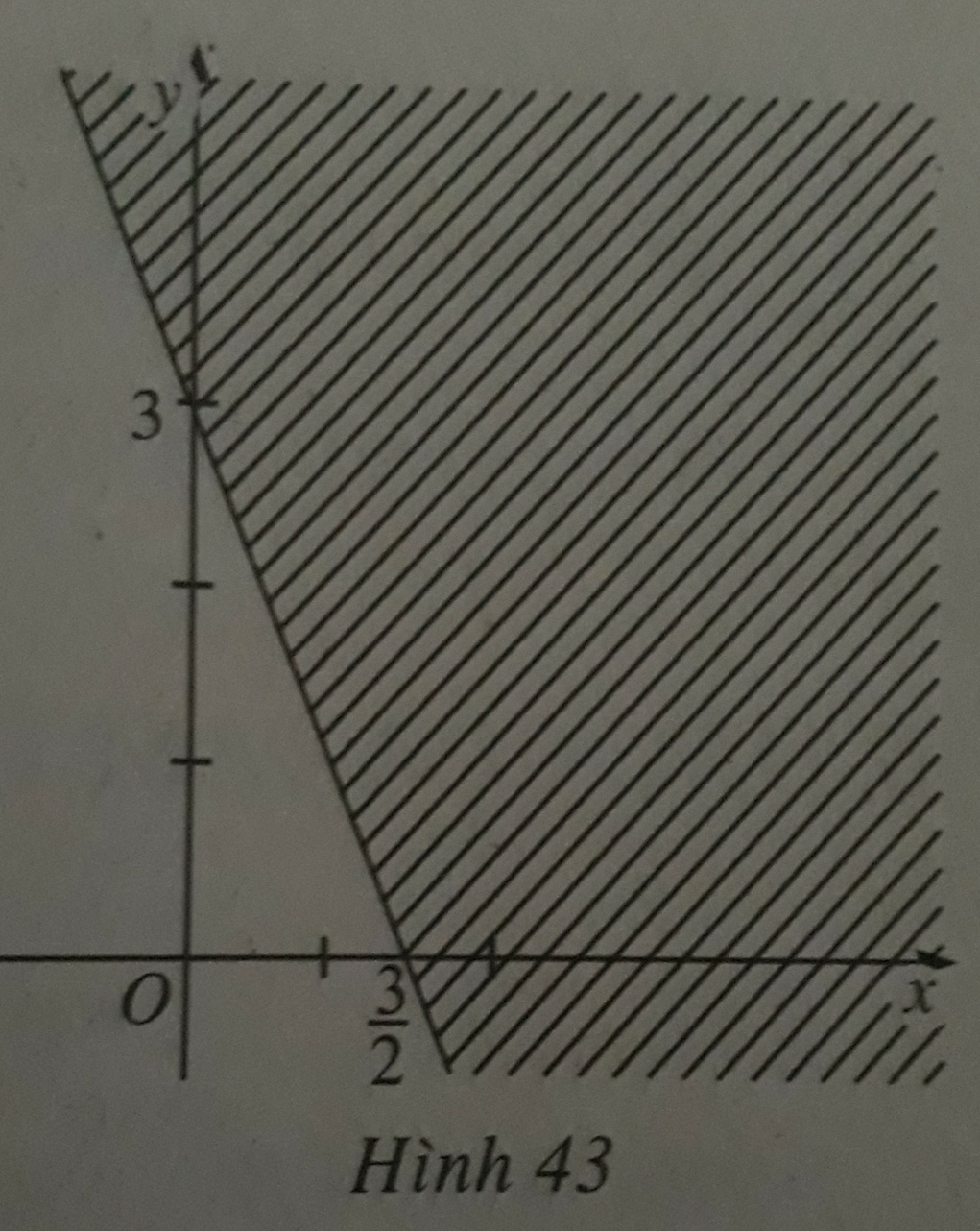
mà theo đề bài \(x+my\ge n\) và đồ thị đề bài cho không thỏa
Vậy bạn nên xem lại đề bài.
Đúng 1
Bình luận (0)
và (x; y) = (-2; 1) là một nghiệm của hệ.
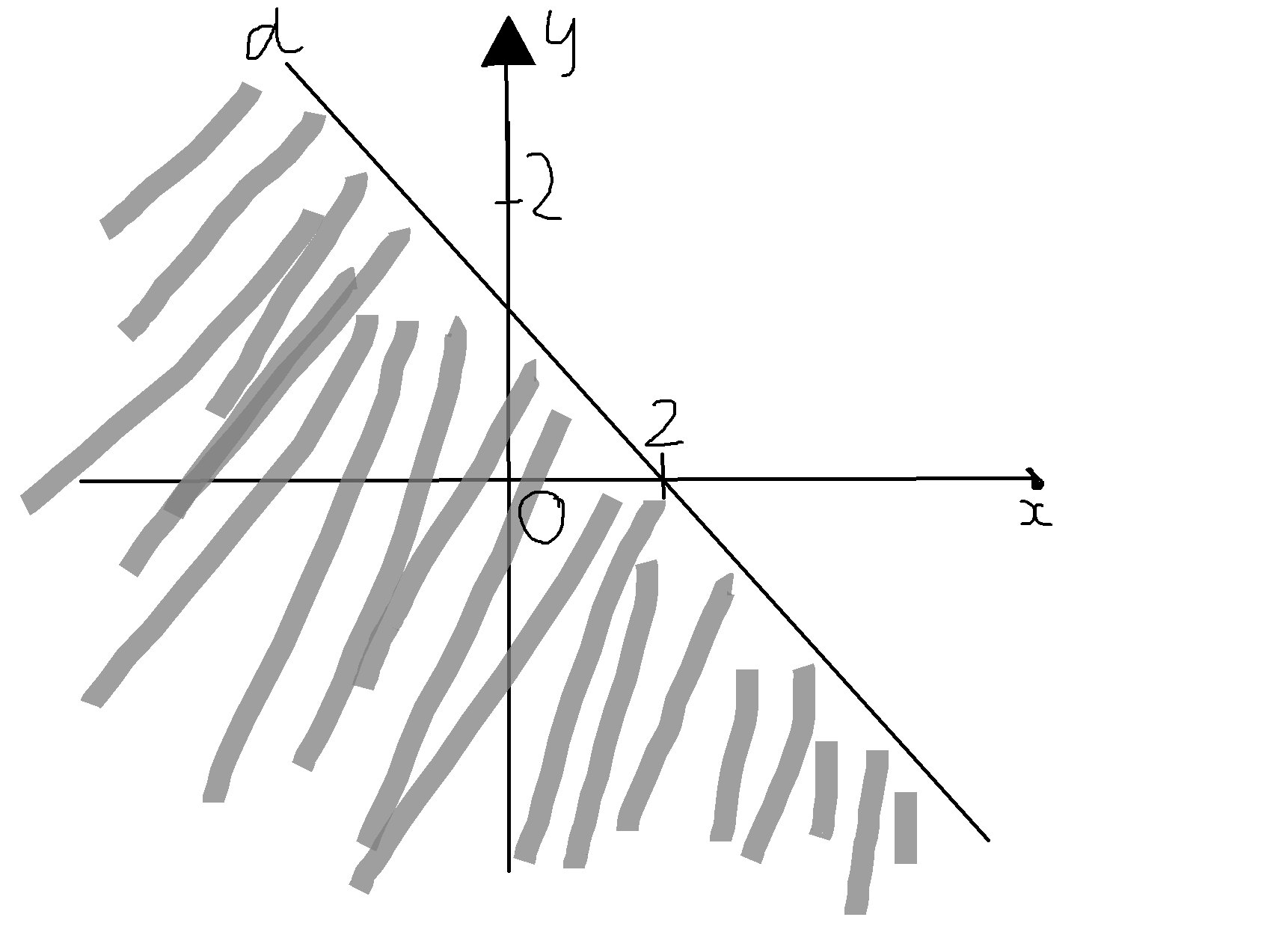
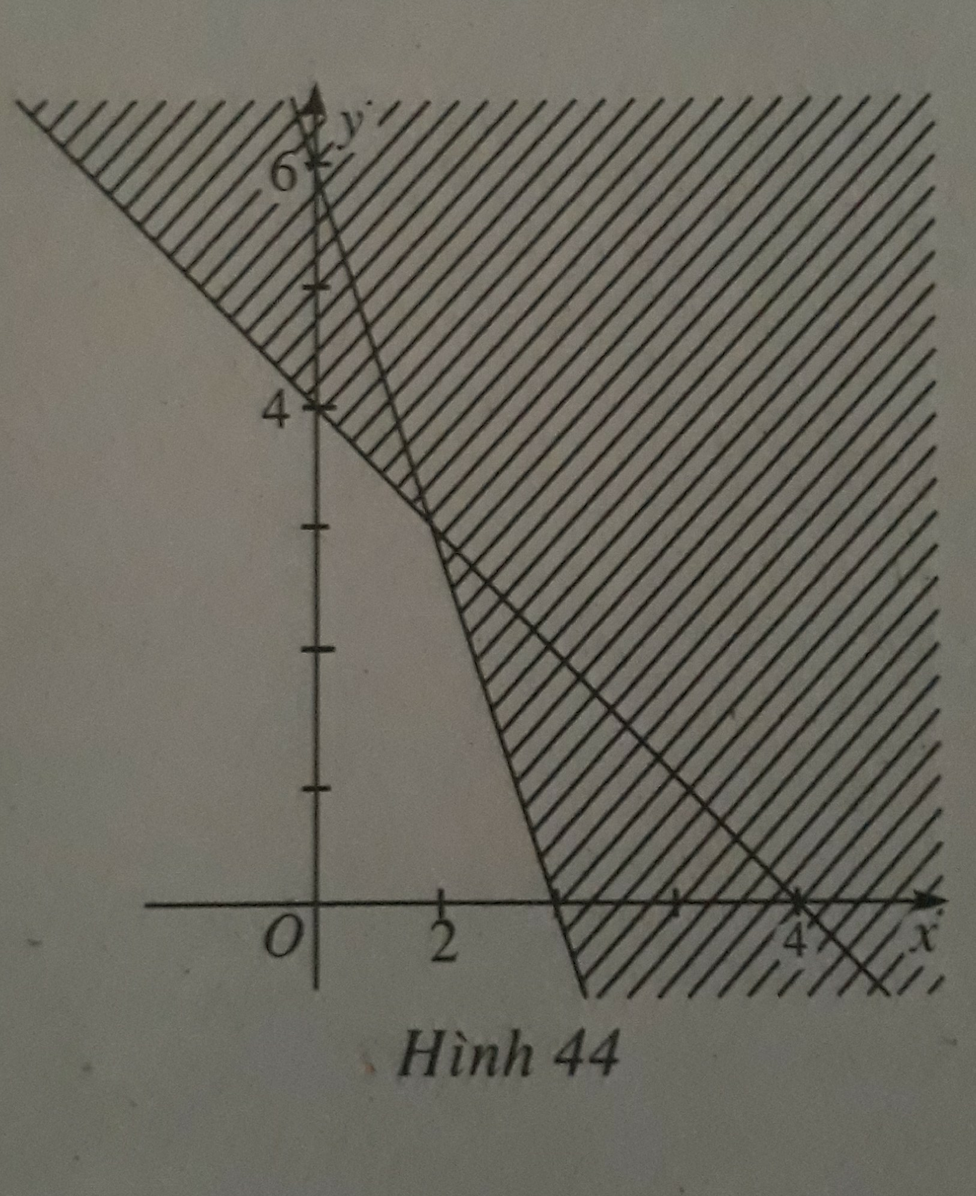
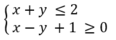và (x; y) = (1; 0) là một nghiệm của hệ.
