a: n(omega)=40
n(A)=20
=>P(A)=20/40=1/2
b: B={3;6;..;39}
=>n(B)=13
=>P(B)=13/40
a: n(omega)=40
n(A)=20
=>P(A)=20/40=1/2
b: B={3;6;..;39}
=>n(B)=13
=>P(B)=13/40
từ một nhóm gồm 6 học sinh nữ và 4 học sinh nam, chọn ngẫu nhiên 3 học sinh. tính xác suất để chọn được 2 học sinh nữ và 1 học sinh nam
Chọn ngẫu nhiên một số có 3 chữ số được lập từ các chữ số 0;1;2;3;4;5. Tính xác suất để số chọn được chia hết cho 3
gọi s là tập hợp tất cả các số tự nhiên có 3 chữ số đôi một khác nhau được lập từ các chữ số 1,2,3,4,5,6. Chọn ngẫu nhiên một số từ S, tính xác suất để số được chọn là 1 số chia hết cho 5
Đội tuyển học sinh giỏi của một trường Trung học phổ thông có 22 học sinh trong đó khối 12 có bẩy học sinh khối 11 có 10 học sinh và khối 10 có năm học sinh nhà trường chọn ngẫu nhiên bẩy học sinh từ đội tuyển đi dự trại hè tính xác suất để a mấy học sinh được chọn có bốn học sinh khối 12 và 3 học sinh khối 11 bê bẩy học sinh được chọn có mặt học sinh cả 3 khối 2 cho Q(x)=x^5 (3x-5)^7 tìm số hạng chứa x^10 trong khai triển của Q(x)
Một hộp chưa 16 quả cầu được đánh số từ 1 đến 16. Lấy ngẫu nhiên 3 quả cầu. Tính xác suất để tổng số ghi trên 3 quả cầu chia hết cho 3.
Thống kê điểm toán của 40 học sinh của một lớp người ta thu được mẫu số liệu ban đầu như sau:
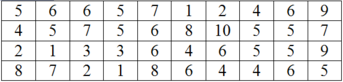
Lập bảng phân bố tần số - tần suất ghép lớp với các lớp như sau:
[1; 2]; [3; 4]; [5; 6]; [7; 8]; [9; 10]
Từ đó; chọn mệnh đề đúng trong các mệnh đề sau?
A. Lớp 2 và 4 có cùng tần số
B. Lớp 5 có tần suất cao nhất
C. Lớp 3 có tần số thấp nhất
D. tất cả sai
một lớp có 40 học sinh . Hỏi có bao nhiêu cách chọn 4 học sinh từ lớp đó để giữ chức vụ 4 tổ trưởng
Để may đồng phục cho khối học sinh lớp năm của một trường tiểu học. Người ta chọn ra một lớp 5A, thống kê chiều cao của 45 học sinh lớp (tính bằng cm) được ghi lại như sau :

Số các giá trị khác nhau của dấu hiệu là:
A. 17
B. 18
C. 19
D. 20