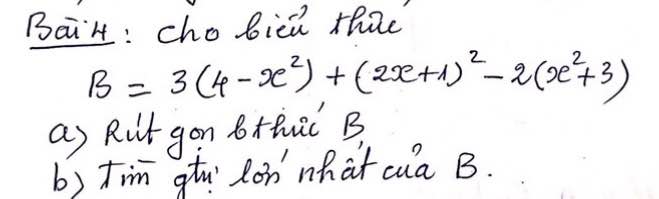Question

Mn ơi giúp em giải câu a với ah

Answer 1

`a)`\(B=3\left(4-x^2\right)+\left(2x+1\right)^2-2\left(x^2+3\right)\)

\(B=12-3x^2+4x^2+4x+1-2x^2-6\)

\(B=-x^2+4x+7\)

`b)`\(B=-x^2+4x+7\)

\(B=-\left(x^2-4x+4\right)+11\)

\(B=-\left(x-2\right)^2+11\le11\)

Dấu "=" xảy ra khi \(x=2\)

Vậy \(Max_B=11\) khi `x=2`

Answer 2

a: \(B=12-3x^2+4x^2+4x+1-2x^2-6\)

\(=-x^2+4x+7\)

b: \(B=-\left(x^2-4x-7\right)\)

\(=-\left(x^2-4x+4-11\right)\)

\(=-\left(x-2\right)^2+11< =11\)

Dấu '=' xảy ra khi x=2

Answer 3

\(a,B=12-3x^2+4x^2+4x+1-2x^2-6=-x^2+4x+7\)

b, \(-\left(x^2-4x-7\right)=-\left(x^2-4x+4\right)+11=-\left(x-2\right)^2+11\)

\(\left(x-2\right)^2\ge0\\ -\left(x-2\right)^2\le0\\ -\left(x-2\right)^2+11\le11\)

Dấu " =" xảy ra khi

\(x-2=0\\ x=2\)

Vậy GTLN B là : 11 khi x =2