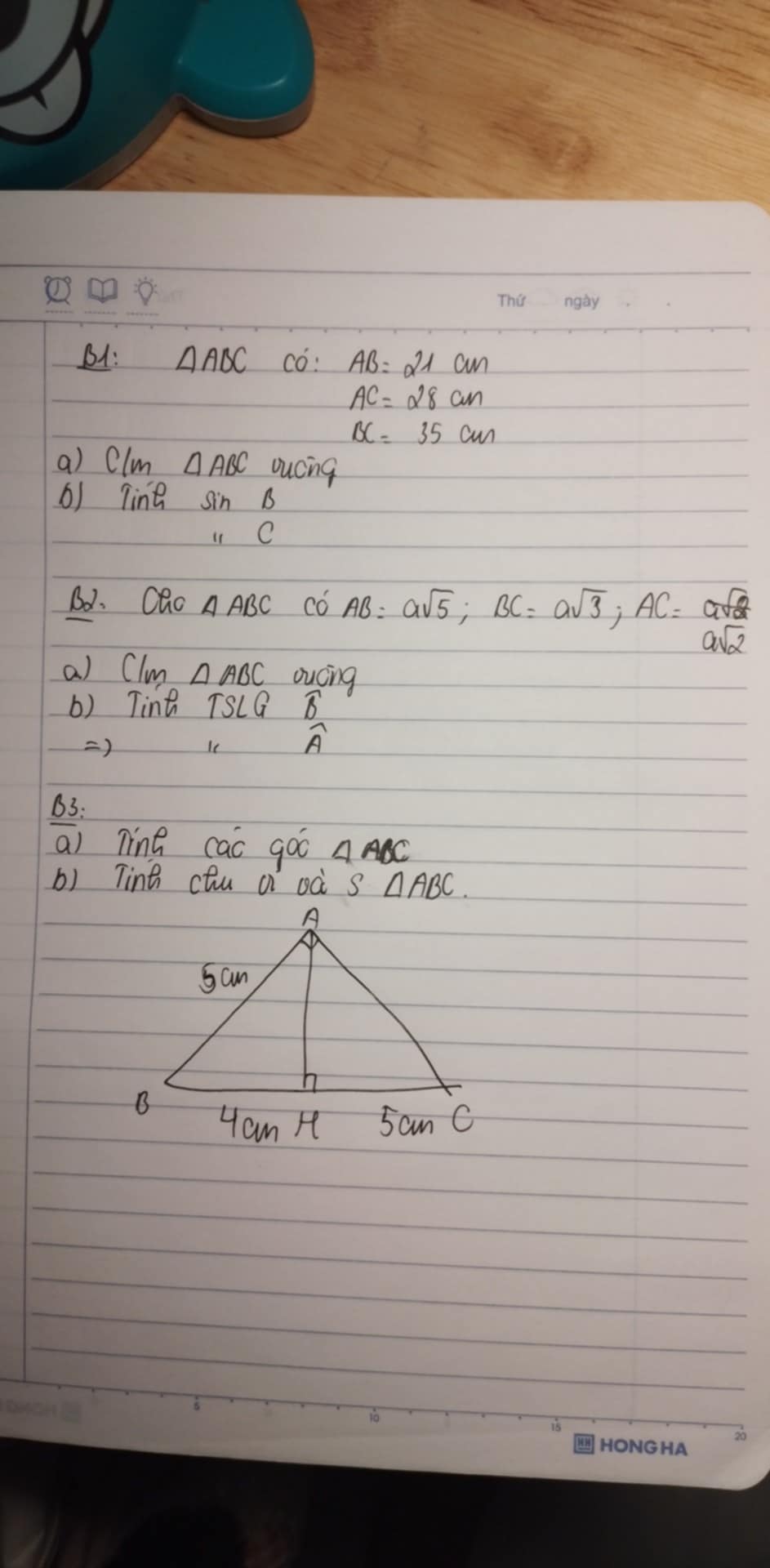
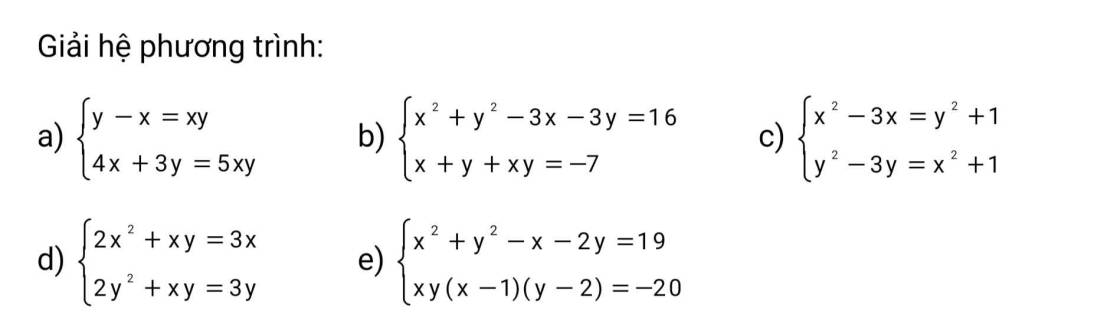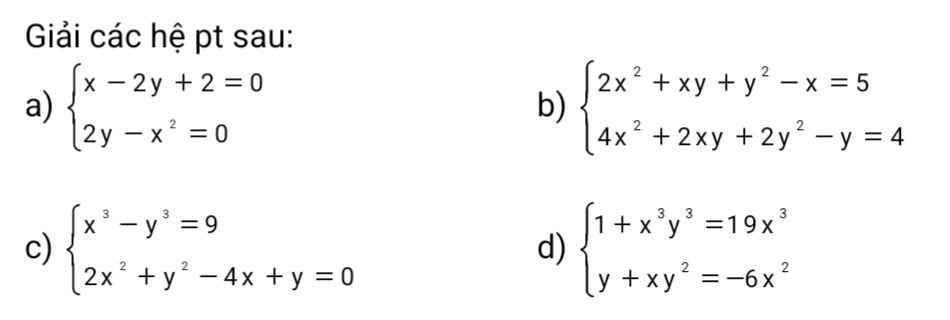Bài 1:
`a)` có :`21^2 + 28^2 = 441 + 784 = 1225`
`35^2 = 1225`
`=> 35^2 = 21^2 + 28^2`
`=>ΔABC `vuông tại `A`
`b)`xét `ΔABC` vuông tại `A` có :
\(\sin B=\dfrac{AC}{BC}=\dfrac{28}{35}=\dfrac{4}{5}\)
`sin C = AC / BC = 21/35 = 3/5`
Bài 2:
có: \(\left(a\sqrt{2}\right)^2+\left(a\sqrt{3}\right)^2=2a^2+3a^2=5a^2\)
\(\left(a\sqrt{5}\right)^2=5a^2\)
`=>`\(\left(a\sqrt{5}\right)^2=\left(a\sqrt{3}\right)^2+\left(a\sqrt{2}\right)^2\)
`=> ΔABC` vuông tại `C`
\(sinB=\dfrac{a\sqrt{2}}{a\sqrt{5}}=\dfrac{\sqrt{10}}{5}\)
\(cosB=\dfrac{a\sqrt{3}}{a\sqrt{5}}=\dfrac{\sqrt{15}}{5}\)
\(tanB=\dfrac{a\sqrt{2}}{a\sqrt{3}}=\dfrac{\sqrt{6}}{3}\)
\(cotB=\dfrac{\sqrt{6}}{2}\)
còn lạ tương tự
Bài 1:
a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
b: Xét ΔABC vuông tại A có
\(sinB=\dfrac{AC}{BC}=\dfrac{28}{35}=\dfrac{4}{5}\)
\(sinC=\dfrac{AB}{BC}=\dfrac{21}{35}=\dfrac{3}{5}\)
Bài 2:
a: XétΔABC có \(AB^2=BC^2+AC^2\)
nên ΔCAB vuông tại C
b: Xét ΔCAB vuông tại C có
\(sinA=cosB=\dfrac{BC}{AB}=\dfrac{a\sqrt{3}}{a\sqrt{5}}=\sqrt{\dfrac{3}{5}}=\dfrac{\sqrt{15}}{5}\)
\(cosA=sinB=\dfrac{AC}{AB}=\dfrac{a\sqrt{2}}{a\sqrt{5}}=\sqrt{\dfrac{2}{5}}=\dfrac{\sqrt{10}}{5}\)
\(tanA=cotB=\dfrac{BC}{AC}=\dfrac{\sqrt{15}}{5}:\dfrac{\sqrt{10}}{5}=\sqrt{\dfrac{15}{10}}=\sqrt{\dfrac{3}{2}}=\dfrac{\sqrt{6}}{2}\)
\(cotA=tanB=\dfrac{AC}{BC}=\dfrac{2}{\sqrt{6}}=\dfrac{2\sqrt{6}}{6}=\dfrac{\sqrt{6}}{3}\)