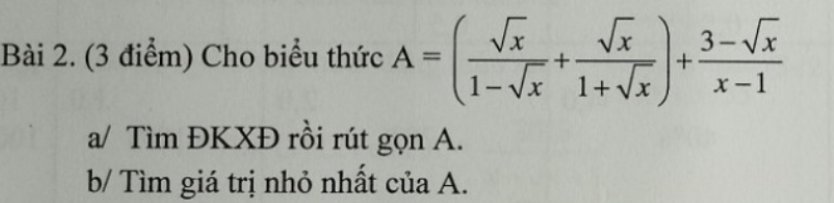a: Xét (O) có
ΔAEB nội tiếp
AB là đường kính
Do đó: ΔAEB vuông tại E
=>AE⊥BE tại E
Xét tứ giác EAOK có \(\hat{AEK}+\hat{AOK}=90^0+90^0=180^0\)
nên EAOK là tứ giác nội tiếp
b: Xét ΔOMA có OM=OA và \(\hat{MOA}=90^0\)
nên ΔMOA vuông cân tại O
=>\(\hat{OAM}=\hat{OMA}=45^0\)
Xét (O) có
\(\hat{MEB};\hat{MAB}\) là các góc nội tiếp chắn cung MB
Do đó: \(\hat{MEB}=\hat{MAB}=45^0\)
Xét (O) có
\(\hat{MAE};\hat{MBE}\) là các góc nội tiếp chắn cung ME
Do đó: \(\hat{MAE}=\hat{MBE}\)
Xét ΔMAE và ΔMBF có
MA=MB
\(\hat{MAE}=\hat{MBF}\)
AE=BF
Do đó: ΔMAE=ΔMBF
=>ME=MF
Xét ΔMEF có ME=MF và \(\hat{MEF}=45^0\)
nên ΔMEF vuông cân tại M
c: Ta có: \(\hat{BEA}=90^0\)
=>BE⊥AE tại E
=>BE⊥AD tại E
=>\(\hat{BED}=90^0\)
=>\(\hat{KED}=2\cdot\hat{KEM}\)
=>EM là phân giác của góc DEK
Xét ΔDEK có EM là phân giác
nên \(\frac{MK}{MD}=\frac{EK}{ED}\)
=>\(MK\cdot ED=MD\cdot EK\)













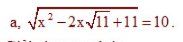


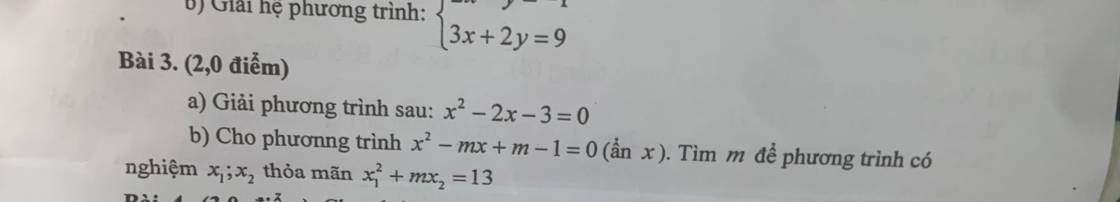



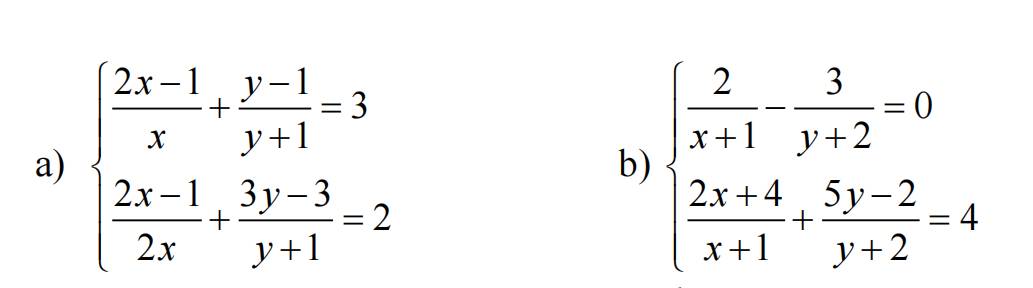



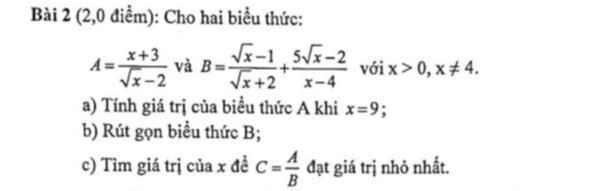 mn giúp mik câu c vs ạ
mn giúp mik câu c vs ạ