hình vẽ: 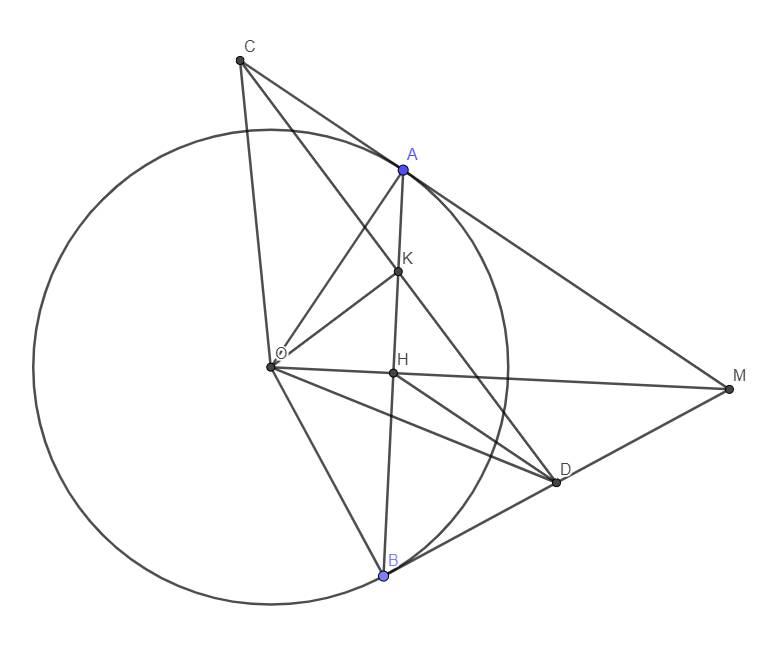
ta có: \(\widehat{OBD}=90^o\)(vì BM là tiếp tuyến tại B của \(\left(O\right)\))
mà \(\widehat{OKC}=90^o\left(gt\right)\)\(\Rightarrow\) tứ giác OKDB nội tiếp \(\Rightarrow\widehat{KBD}=\widehat{KOD}\)
mà \(\widehat{KBD}=\widehat{BAM}=\widehat{COK}\)\(\Rightarrow\widehat{COK}=\widehat{KOD}\)
Từ đó chứng minh được \(\Delta KOC=\Delta KOD\left(g.c.g\right)\Rightarrow KD=KC\)
Xét \(\Delta KHD\) và \(\Delta KCA\)
\(AK=KH\left(gt\right)\)
\(CK=KD\left(cmt\right)\)
\(\widehat{CKA}=\widehat{DKH}\left(dd\right)\)
\(\Rightarrow\Delta KHD=\Delta KCA\left(g.c.g\right)\Rightarrow\widehat{ACK}=\widehat{KDH}\Rightarrow AM\text{//}DH
\)
mà \(AH=HB\left(gt\right)\Rightarrow BD=DM\left(dtb\right)\Rightarrowđpcm\)
Đúng 1
Bình luận (0)
Các câu hỏi tương tự
làm ý 2 thôi nhé
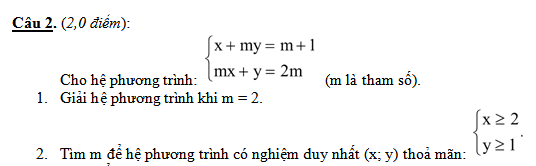
Giúp tôi 2 đến 3 bài thôi nhé ( xin cảm ơn trước )
chỉ cần làm 2 ý đầu thôi nhé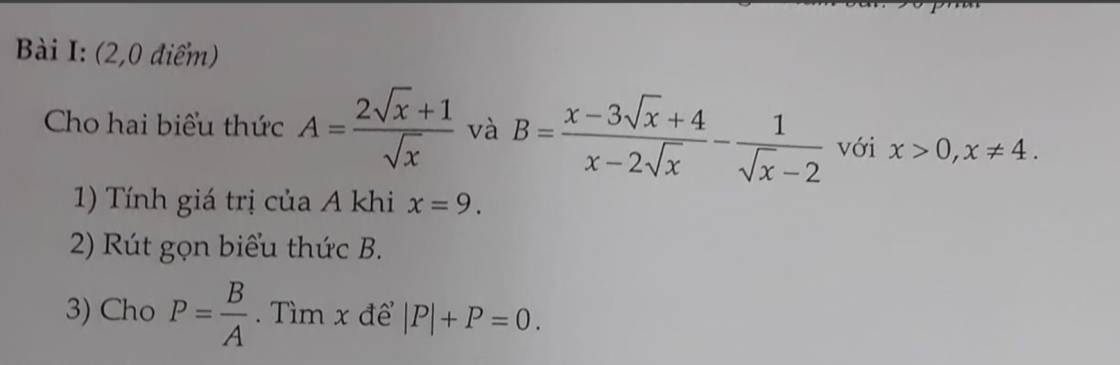
Mình sắp thi lên 10 nên muốn xin những câu hình hay để học. Ai có đề Toán THPT cho mình xin câu hình có ý cuối hay hay tí ạ. Mơn nhìu:)
MN GIÚP MIK CÂU Ý 3 THÔI Ạ
MIK CHỈ CẦN Ý 3 THÔI Ạ
KO CẦN Ý 1,2 Ạ

Giúp mik câu b,c thôi nhé,cảm ơn <3
Cho đường tròn (O), đường kính AB cố định, điểm I nằm giữa A và O sao cho AI2/3AO . Kẻ dây MN vuông góc với AB tại I. Gọi C là điểm tùy ý thuộc cung lớn MN sao cho C không trùng với M,N và B. Nối AC cắt MN tại Ea) Chứn minh tứ giác IECB nội tiếpb) Chứng minh rằng AM ^2 AE. ACc) Xác định vị trí của điểm C sao cho khoảng cách từ N đến tâm đương tròn ngoại tiếp tam giác CME là nhỏ nhất. Tính giá trị nhỏ nhất ấy theo R.Mình chỉ xin câu c thôi ạ
Đọc tiếp
Cho đường tròn (O), đường kính AB cố định, điểm I nằm giữa A và O sao cho AI=2/3AO . Kẻ dây MN vuông góc với AB tại I. Gọi C là điểm tùy ý thuộc cung lớn MN sao cho C không trùng với M,N và B. Nối AC cắt MN tại E
a) Chứn minh tứ giác IECB nội tiếp
b) Chứng minh rằng AM ^2 = AE. AC
c) Xác định vị trí của điểm C sao cho khoảng cách từ N đến tâm đương tròn ngoại tiếp tam giác CME là nhỏ nhất. Tính giá trị nhỏ nhất ấy theo R.
Mình chỉ xin câu c thôi ạ
Xin lỗi AD và các bạn học Toán nhé vì câu hỏi này ko liên quan đến Toán ^_^
Các bạn cho mình hỏi đã bạn nào KT 1 Tiếng Anh 9 - bài 1 2 chưa nếu rồi cho mình mượn đề. Xin cảm ơn nhiều -_-
Cho (P):y = ax2 và A (2; -2)
a) Xác định a biết a thuộc (P)
b) Tìm các điểm M thuộc (P) có hoành độ hơn tung độ 4 đơn vị
Mọi người cho mình xin câu b thôi ạ
Cho đường tròn (O) có đường kính AB 2R, dây CD vuông góc với OA tại trung điểm M của OA. Tieeso tuyến tại C của (O) cắt OA tại N.a) Chứng minh tứ giác ACOD là hình thoi. Tính số đo góc COA và độ dài CN theo R.b) Vè đường tròn tâm D bán kính DM cắt đường tròn (O) tại E và F. Vẽ đường kính DP của (O), DP cắt BC tại I và cắt FE tại H. Chứng minh I là trung điểm BC và BC song song với FE.c) Gọi K là trung điểm DM. Chứng minh E, K, F thẳng hàng. mọi người cho mình xin câu b ý 2 và câu c th...
Đọc tiếp
Cho đường tròn (O) có đường kính AB = 2R, dây CD vuông góc với OA tại trung điểm M của OA. Tieeso tuyến tại C của (O) cắt OA tại N.
a) Chứng minh tứ giác ACOD là hình thoi. Tính số đo góc COA và độ dài CN theo R.
b) Vè đường tròn tâm D bán kính DM cắt đường tròn (O) tại E và F. Vẽ đường kính DP của (O), DP cắt BC tại I và cắt FE tại H. Chứng minh I là trung điểm BC và BC song song với FE.
c) Gọi K là trung điểm DM. Chứng minh E, K, F thẳng hàng.
mọi người cho mình xin câu b ý 2 và câu c thôi ạ, mình cảm ơn nhiều


 Mình xin ý 2 câu c thôi nhé
Mình xin ý 2 câu c thôi nhé










