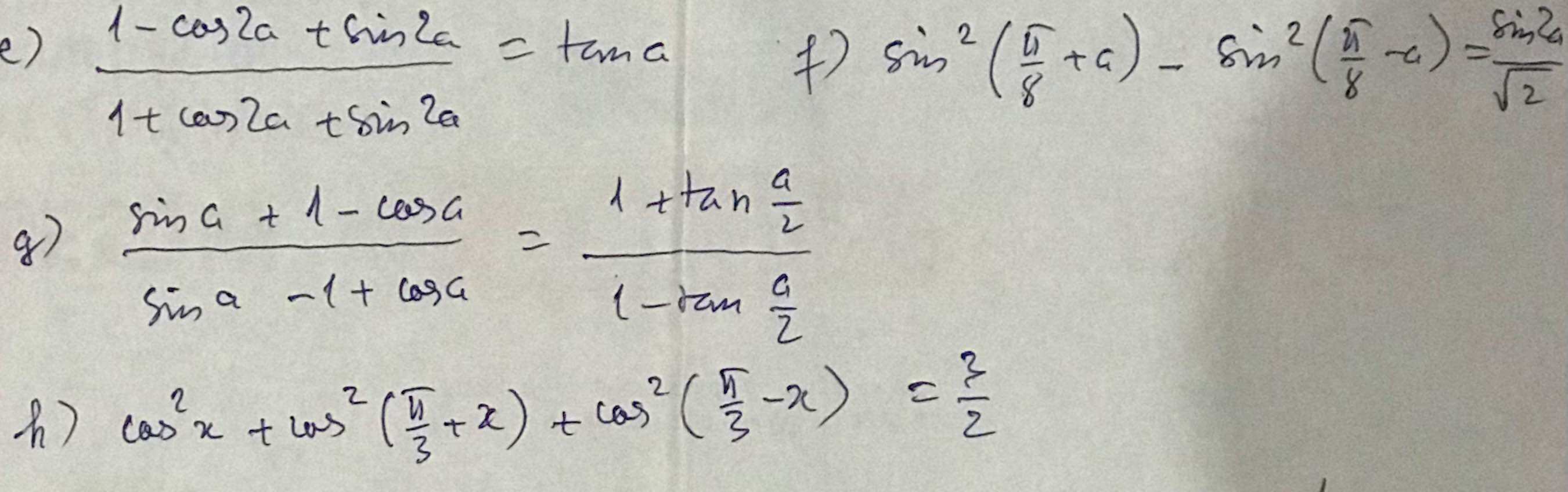g: \(\dfrac{sina+1-cosa}{sina-1+cosa}\)
\(=\dfrac{2\cdot sin\left(\dfrac{a}{2}\right)\cdot cos\left(\dfrac{a}{2}\right)+1-cos\left(2\cdot\dfrac{a}{2}\right)}{2\cdot sin\left(\dfrac{a}{2}\right)\cdot cos\left(\dfrac{a}{2}\right)-1+cos\left(2\cdot\dfrac{a}{2}\right)}\)
\(=\dfrac{2\cdot sin\left(\dfrac{a}{2}\right)\cdot cos\left(\dfrac{a}{2}\right)+2\cdot sin^2\left(\dfrac{a}{2}\right)}{2\cdot sin\left(\dfrac{a}{2}\right)\cdot cos\left(\dfrac{a}{2}\right)-2\cdot sin^2\left(\dfrac{a}{2}\right)}\)
\(=\dfrac{2\cdot sin\left(\dfrac{a}{2}\right)\cdot\left(cos\left(\dfrac{a}{2}\right)+sin\left(\dfrac{a}{2}\right)\right)}{2\cdot sin\left(\dfrac{a}{2}\right)\cdot\left(cos\left(\dfrac{a}{2}\right)-sin\left(\dfrac{a}{2}\right)\right)}=\dfrac{cos\left(\dfrac{a}{2}\right)+sin\left(\dfrac{a}{2}\right)}{cos\left(\dfrac{a}{2}\right)-sin\left(\dfrac{a}{2}\right)}\)
\(=\dfrac{\dfrac{cos\left(\dfrac{a}{2}\right)}{cos\left(\dfrac{a}{2}\right)}+\dfrac{sin\left(\dfrac{a}{2}\right)}{cos\left(\dfrac{a}{2}\right)}}{\dfrac{cos\left(\dfrac{a}{2}\right)}{cos\left(\dfrac{a}{2}\right)}-\dfrac{sin\left(\dfrac{a}{2}\right)}{cos\left(\dfrac{a}{2}\right)}}=\dfrac{1+tan\left(\dfrac{a}{2}\right)}{1-tan\left(\dfrac{a}{2}\right)}\)
h: \(cos^2x+cos^2\left(x+\dfrac{\Omega}{3}\right)+cos^2\left(\dfrac{\Omega}{3}-x\right)\)
\(=cos^2x+\left[cosx\cdot cos\left(\dfrac{\Omega}{3}\right)-sinx\cdot sin\left(\dfrac{\Omega}{3}\right)\right]^2+\left[cos\left(\dfrac{\Omega}{3}\right)\cdot cosx+sin\left(\dfrac{\Omega}{3}\right)\cdot sinx\right]^2\)
\(=cos^2x+\left(\dfrac{1}{2}cosx-\dfrac{\sqrt{3}}{2}sinx\right)^2+\left(\dfrac{1}{2}cosx+\dfrac{\sqrt{3}}{2}\cdot sinx\right)^2\)
\(=cos^2x+\dfrac{1}{4}cos^2x+\dfrac{3}{4}sin^2x+\dfrac{1}{4}cos^2x+\dfrac{3}{4}sin^2x\)
\(=\dfrac{3}{2}sin^2x+\dfrac{3}{2}cos^2x=\dfrac{3}{2}\)
e: \(\dfrac{1-cos2a+sin2a}{1+cos2a+sin2a}\)
\(=\dfrac{1-\left(2\cdot cos^2a-1\right)+2\cdot cosa\cdot sina}{1+2cos^2a-1+2\cdot cosa\cdot sina}\)
\(=\dfrac{1-\left(1-2sin^2a\right)+2\cdot cosa\cdot sina}{2cos^2a+2\cdot cosa\cdot sina}\)
\(=\dfrac{2\cdot sin^2a+2\cdot cosa\cdot sina}{2\cdot cos^2a+2\cdot cosa\cdot sina}\)
\(=\dfrac{2\cdot sina\left(sina+cosa\right)}{2\cdot cosa\left(sina+cosa\right)}=\dfrac{sina}{cosa}=tana\)