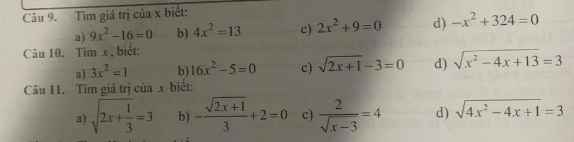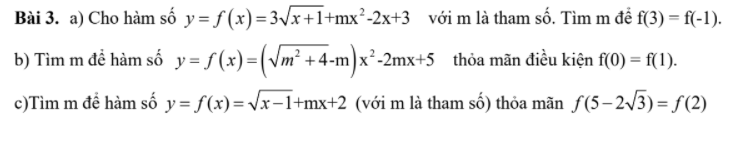\(2,\dfrac{\sqrt{x}}{\sqrt{x}+3}+\dfrac{2\sqrt{x}}{\sqrt{x}-3}-\dfrac{3x+9}{x-9}\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)+2\sqrt{x}\left(\sqrt{x}+3\right)-3x-9}{x-9}\)
\(=\dfrac{x-3\sqrt{x}+2x+6\sqrt{x}-3x-9}{x-9}\)
\(=\dfrac{3\sqrt{x}-9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(=\dfrac{3\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(=\dfrac{3}{\sqrt{x}+3}\)
\(b,M=A.B=\dfrac{\sqrt{x}+3}{3\sqrt{x}}.\dfrac{3}{\sqrt{x}+3}=\dfrac{1}{\sqrt{x}}\)
Thay \(\dfrac{1}{\sqrt{x}}\) vào M trong biểu thức :
\(\Rightarrow\dfrac{1}{\sqrt{x}}.x+2x-3\sqrt{x}=4\sqrt{x+3}-8\)
\(\Rightarrow\dfrac{x+2x\sqrt{x}-3x-4\sqrt{x}.\sqrt{x+3}-8\sqrt{x}}{\sqrt{x}}=0\)
\(\Rightarrow x=0\)
1: Khi x=4 thì \(A=\dfrac{2+3}{3\cdot2}=\dfrac{5}{6}\)
2: \(=\dfrac{x-3\sqrt{x}+2x+6\sqrt{x}-3x-9}{x-9}=\dfrac{-3\left(\sqrt{x}-3\right)}{x-9}=\dfrac{-3}{\sqrt{x}+3}\)
3: \(M=A\cdot B=\dfrac{-3}{\sqrt{x}+3}\cdot\dfrac{\sqrt{x}+3}{3\sqrt{x}}=\dfrac{-1}{\sqrt{x}}\)
3: \(M\cdot x+2x-3\sqrt{x}=4\sqrt{x+3}-8\)
=>\(4\sqrt{x+3}-8=-\sqrt{x}+2x-3\sqrt{x}=2x-4\sqrt{x}\)
\(\Leftrightarrow2\sqrt{x+3}-4=x-2\sqrt{x}\)
=>2 căn x+3+2 căn x=x+4
=>4(x+3)+4x+8 căn x(x+3)=x+4
=>\(8\cdot\sqrt{x\left(x+3\right)}=x+4-4x-12-4x-8=-7x-16\)
=>\(64x\left(x+3\right)=\left(-7x-16\right)^2=\left(7x+16\right)^2\)
=>\(64x^2+192x-49x^2-224x-256=0\)
=>\(15x^2-32x-256=0\)
=>x=16/3
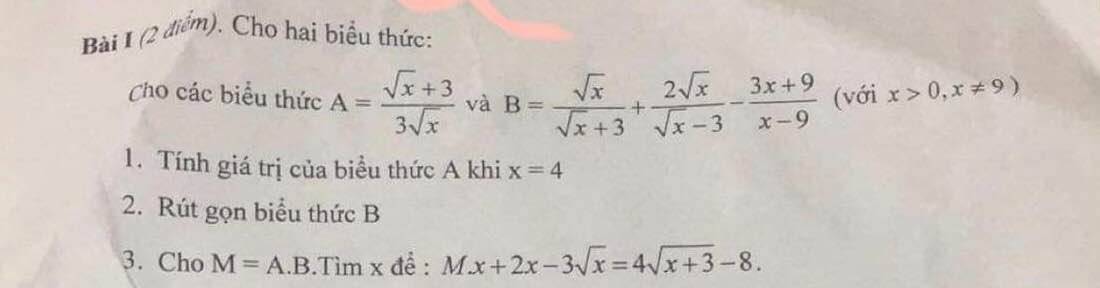
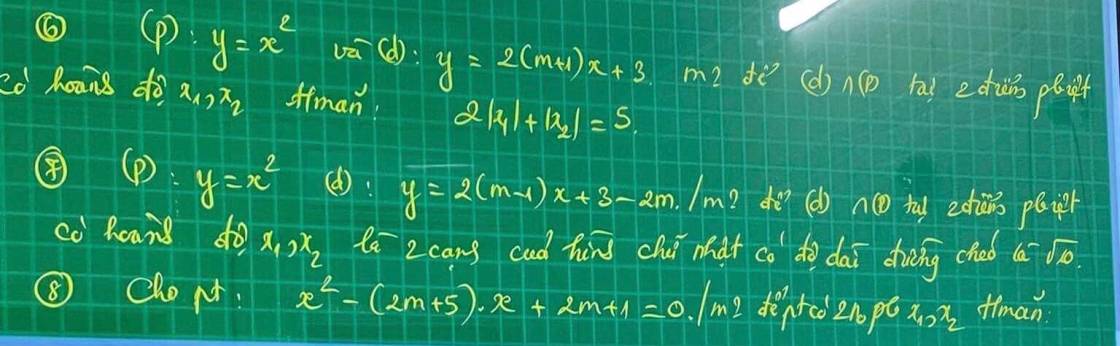
Mọi người giúp mình câu 3, câu 4 với. Mình cảm ơn ạ. Mình đang cần gấp lắm!!!
