Bài 11:
a: Ta có: \(P=\dfrac{x^2-\sqrt{x}}{x+\sqrt{x}+1}\)
\(=\sqrt{x}\cdot\left(\sqrt{x}-1\right)\)
\(=x-\sqrt{x}\)
b: Để P=2 thì \(x-\sqrt{x}-2=0\)
hay x=4
Bài 10:
a: Ta có: \(A=\left(1+\dfrac{\sqrt{x}}{x+1}\right):\left(\dfrac{1}{\sqrt{x}-1}-\dfrac{2\sqrt{x}}{x\sqrt{x}+\sqrt{x}-x-1}\right)\)
\(=\dfrac{x+\sqrt{x}+1}{x+1}:\dfrac{x-2\sqrt{x}+1}{\left(x+1\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{x+\sqrt{x}+1}{x+1}\cdot\dfrac{x+1}{\sqrt{x}-1}\)
\(=\dfrac{x+\sqrt{x}+1}{\sqrt{x}-1}\)
b: Để A<0 thì \(\sqrt{x}-1< 0\)
hay x<1
Kết hợp ĐKXĐ, ta được: \(0\le x< 1\)
Để A=-1 thì \(x+\sqrt{x}+1=-\sqrt{x}+1\)
\(\Leftrightarrow x=0\)
c: Thay x=4 vào A, ta được:
\(A=\dfrac{4+2+1}{2-1}=7\)






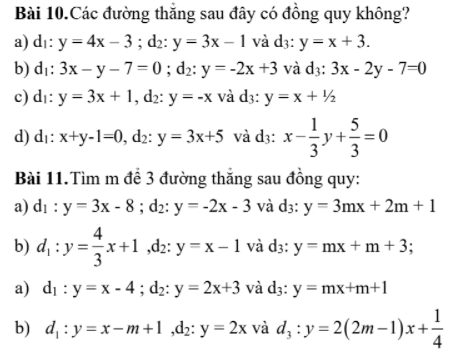

 , mình đang cần giải gấp. Cảm ơn mn nhiều.
, mình đang cần giải gấp. Cảm ơn mn nhiều.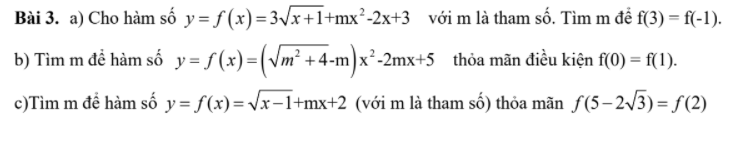



 Mọi người giúp mình câu 3, câu 4 với. Mình cảm ơn ạ. Mình đang cần gấp lắm!!!
Mọi người giúp mình câu 3, câu 4 với. Mình cảm ơn ạ. Mình đang cần gấp lắm!!!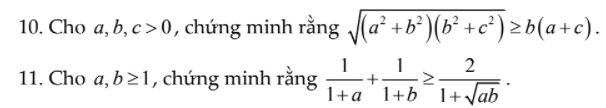
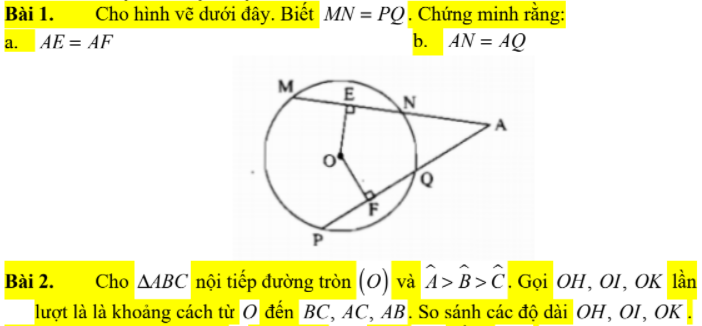
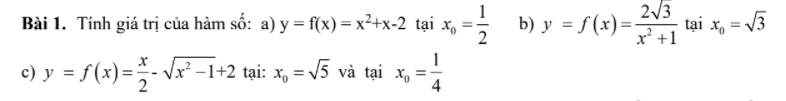 , mình đang cần để nộp ạ. Cảm ơn mn nhiều.
, mình đang cần để nộp ạ. Cảm ơn mn nhiều.