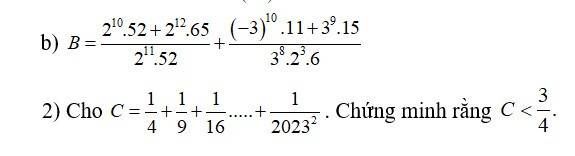b) \(B=\dfrac{2^{10}\cdot52+2^{12}\cdot65}{2^{11}\cdot52}+\dfrac{\left(-3\right)^{10}\cdot11+3^9\cdot15}{3^8\cdot2^3\cdot6}\)
\(B=\dfrac{2^{10}\cdot2^2\cdot13+2^{12}\cdot5\cdot13}{2^{11}\cdot13\cdot2^2}+\dfrac{\left(-3\right)^{10}\cdot11+3^9\cdot3\cdot5}{3^8\cdot2^3\cdot2\cdot3}\)
\(B=\dfrac{2^{12}\cdot13+2^{12}\cdot13\cdot5}{2^{13}\cdot13}+\dfrac{3^{10}\cdot11+3^{10}\cdot5}{3^9\cdot2^4}\)
\(B=\dfrac{2^{12}\cdot13\cdot\left(1+5\right)}{2^{13}\cdot13}+\dfrac{3^{10}\cdot\left(11+5\right)}{3^9\cdot2^4}\)
\(B=\dfrac{1+5}{2}+\dfrac{3\cdot16}{2^4}\)
\(B=3+3\)
\(B=6\)
b) \(B=\dfrac{2^{10}.\left(2^2.13\right)+2^{12}.\left(5.13\right)}{2^{11}.\left(2^2.13\right)}+\dfrac{3^{10}.11+3^9\left(11+4\right)}{3^8.2^4.3}\)
= \(\dfrac{2^{12}.13+2^{12}.5.13}{2^{13}.13}+\dfrac{3^{10}.11+3^9.11.4}{3^9.2^4}\)
= \(\dfrac{2^{12}.13\left(1+5\right)}{2^{12}.13.2}+\dfrac{3^9.11\left(3+4\right)}{3^9.2^4}\)
= \(\dfrac{6}{2}+\dfrac{11.7}{16}\)
= 3 + 77/16 = 125/16
Vậy B = 125/16