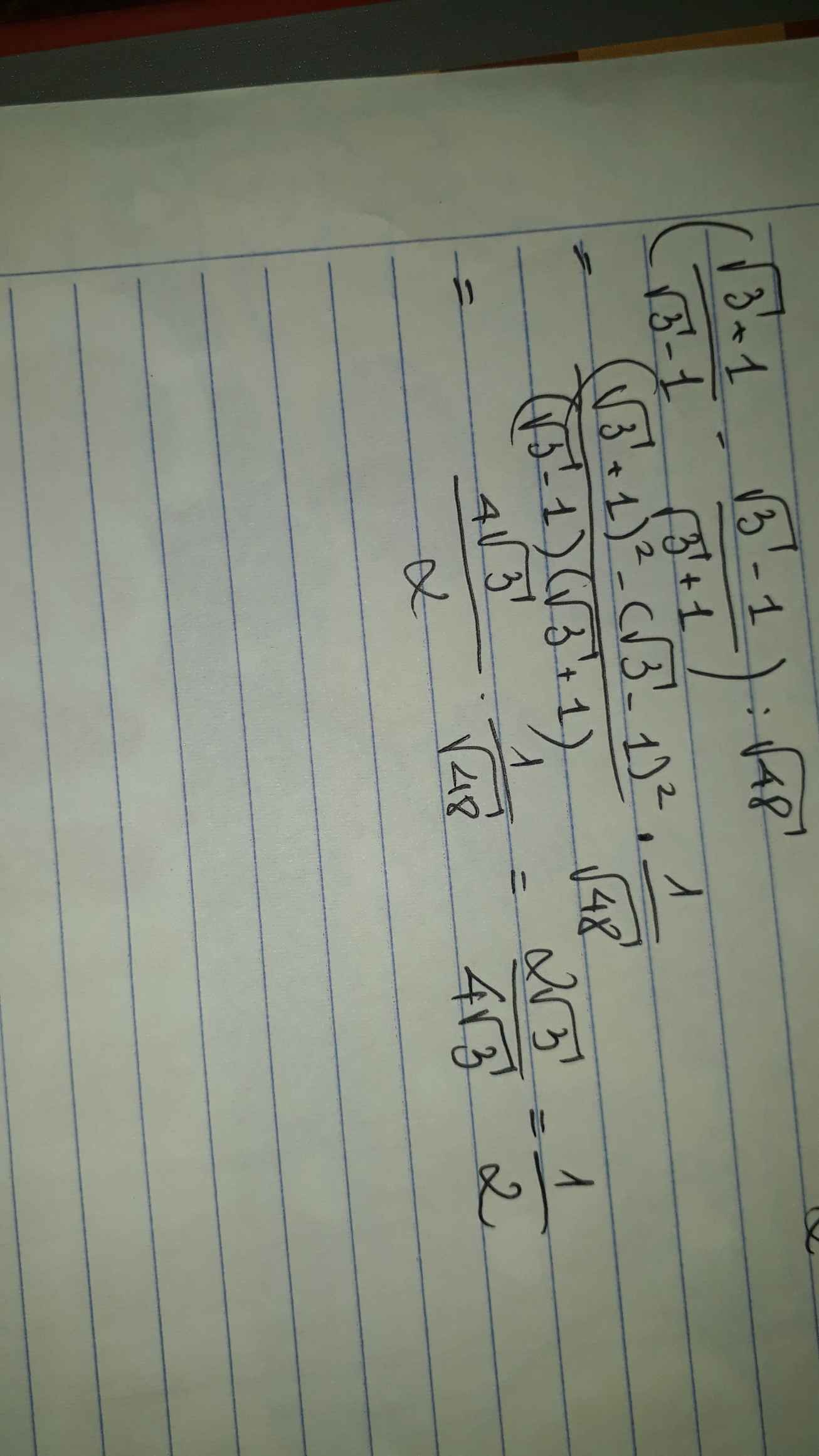Các câu hỏi tương tự
\(\dfrac{1}{3\left(1+\sqrt{2}\right)}+\dfrac{1}{5\left(\sqrt{2}+\sqrt{3}\right)}+\dfrac{1}{7\left(\sqrt{3}+\sqrt{4}\right)}+...+\dfrac{1}{97\left(\sqrt{48}+\sqrt{49}\right)}< \dfrac{7}{3}\)
chứng minh rằng:\(\dfrac{1}{3\left(\sqrt{1}+\sqrt{2}\right)}+\dfrac{1}{5\left(\sqrt{2}+\sqrt{3}\right)}+\dfrac{1}{7\left(\sqrt{3}+\sqrt{4}\right)}+...+\dfrac{1}{97\left(\sqrt{48}+\sqrt{49}\right)}< \dfrac{3}{7}\)
Tính: a, \(\left(4\sqrt{2}-\dfrac{11}{2}\sqrt{8}-\dfrac{1}{3}\sqrt{288}+\sqrt{50}\right)\left(\dfrac{1}{2}\sqrt{2}\right)\)
b, \(\left(\dfrac{4}{5}\sqrt{5}-\dfrac{1}{3}\sqrt{\dfrac{1}{5}}+3\sqrt{20}+\dfrac{1}{2}\sqrt{245}\right)\div\sqrt{5}\)
16 tháng 8 2021 lúc 16:23
giúp tui
a) \(\sqrt{\left(\sqrt{2}+1\right)^2}-\sqrt{3-2\sqrt{2}}\)
b) \(\left(2\sqrt{3}+1\right)^2-\dfrac{1}{4}\sqrt{48}-\dfrac{2}{\sqrt{3}-1}\)
2 tháng 6 2021 lúc 8:27
a.\(\sqrt{28a^4}\)
b. A=\(\left(\dfrac{\sqrt{21}-\sqrt{7}}{\sqrt{3-1}}+\dfrac{\sqrt{10}-\sqrt{5}}{\sqrt{2}-1}\right)\)\(\div\)\(\dfrac{1}{\sqrt{7}-\sqrt{5}}\)
c.\(\left\{{}\begin{matrix}\dfrac{3}{2x}-y=6\\\dfrac{1}{x}+2y=-4\end{matrix}\right.\)
7 tháng 9 2023 lúc 22:51
Thực hiện phép tính và thu gọn biểu thức:
B= \(\left(\dfrac{4}{1-\sqrt{5}}+\dfrac{1}{2+\sqrt{5}}-\dfrac{4}{3-\sqrt{5}}\right)\left(\sqrt{5}-6\right)\)
Thực hiện phép tính:
\(\sqrt{48}-\dfrac{\sqrt{21}-\sqrt{15}}{\sqrt{7}-\sqrt{5}}+\dfrac{2}{\sqrt{3}+1}\)
Thực hiện phép tính:a) (dfrac{6}{sqrt{3}} - 2sqrt{48}) (sqrt{3} - 1)b) dfrac{left(sqrt{5}-1right)^2}{sqrt{5}-3} - sqrt{9-4sqrt{5}}c) 3sqrt{2a} - sqrt{18a^3} + 4sqrt{dfrac{a}{2}} - dfrac{1}{4}sqrt{128a} với a ge 0
Đọc tiếp
Thực hiện phép tính:
a) (\(\dfrac{6}{\sqrt{3}}\) - 2\(\sqrt{48}\)) (\(\sqrt{3}\) - 1)
b) \(\dfrac{\left(\sqrt{5}-1\right)^2}{\sqrt{5}-3}\) - \(\sqrt{9-4\sqrt{5}}\)
c) 3\(\sqrt{2a}\) - \(\sqrt{18a^3}\) + 4\(\sqrt{\dfrac{a}{2}}\) - \(\dfrac{1}{4}\)\(\sqrt{128a}\) với a \(\ge\) 0
Bài 1: Thực hiện phép tính:a, left(sqrt{24}-sqrt{48}-sqrt{6}right)sqrt{6}+12sqrt{2}b, left(sqrt{dfrac{1}{5}}-sqrt{dfrac{16}{5}}+sqrt{5}right):sqrt{20}c, sqrt{21+3sqrt{48}}-sqrt{21-3sqrt{48}}Bài 2: Giải các phương trình sau:a, dfrac{1}{3}sqrt{x-2}-dfrac{2}{3}sqrt{9x-18}+6sqrt{dfrac{x-2}{81}}-4b, sqrt{9x^2+12x
+4}4xc, sqrt{x-2sqrt{x-1}}sqrt{x-1}GIÚP MIK VỚIIII
Đọc tiếp
Bài 1: Thực hiện phép tính:
a, \(\left(\sqrt{24}-\sqrt{48}-\sqrt{6}\right)\sqrt{6}+12\sqrt{2}\)
b, \(\left(\sqrt{\dfrac{1}{5}}-\sqrt{\dfrac{16}{5}}+\sqrt{5}\right):\sqrt{20}\)
c, \(\sqrt{21+3\sqrt{48}}-\sqrt{21-3\sqrt{48}}\)
Bài 2: Giải các phương trình sau:
a, \(\dfrac{1}{3}\sqrt{x-2}-\dfrac{2}{3}\sqrt{9x-18}+6\sqrt{\dfrac{x-2}{81}}=-4\)
b, \(\sqrt{9x^2+12x +4}=4x\)
c, \(\sqrt{x-2\sqrt{x-1}}=\sqrt{x-1}\)
GIÚP MIK VỚIIII
29 tháng 11 2023 lúc 16:02
Bài 1: Tínha) sqrt{27}+dfrac{1}{2}sqrt{48}-sqrt{108} b) left(sqrt{14}-sqrt{10}right)sqrt{6+sqrt{35}} c) dfrac{sqrt{15}+sqrt{3}}{1+sqrt{5}}-dfrac{2}{sqrt{3}-1} Bài 2: Cho biểu thức A dfrac{x-5}{x+2sqrt{x}-3}+dfrac{1}{sqrt{x}+3}+dfrac{2}{sqrt{x}-1} a) Rút gọn Ab) Tìm x để A 2c) Tìm các số nguyên của x để A ∈ Z
Đọc tiếp
Bài 1: Tính
a) \(\sqrt{27}+\dfrac{1}{2}\sqrt{48}-\sqrt{108}\)
b) \(\left(\sqrt{14}-\sqrt{10}\right)\sqrt{6+\sqrt{35}}\)
c) \(\dfrac{\sqrt{15}+\sqrt{3}}{1+\sqrt{5}}-\dfrac{2}{\sqrt{3}-1}\)
Bài 2: Cho biểu thức
A = \(\dfrac{x-5}{x+2\sqrt{x}-3}+\dfrac{1}{\sqrt{x}+3}+\dfrac{2}{\sqrt{x}-1}\)
a) Rút gọn A
b) Tìm x để A = 2
c) Tìm các số nguyên của x để A ∈ Z
\(\left(1+\sqrt{3}-\sqrt{2}\right)\left(1+\sqrt{3}-\sqrt{2}\right)\)
\(\left(1+\dfrac{5-\sqrt{5}}{1-\sqrt{5}}\right)\left(\dfrac{5+\sqrt{5}}{1+\sqrt{5}}+1\right)\)
\(\left(\dfrac{1}{\sqrt{3}-\sqrt{2}}\right)\left(\dfrac{1}{\sqrt{3}-\sqrt{2}}\right)\)