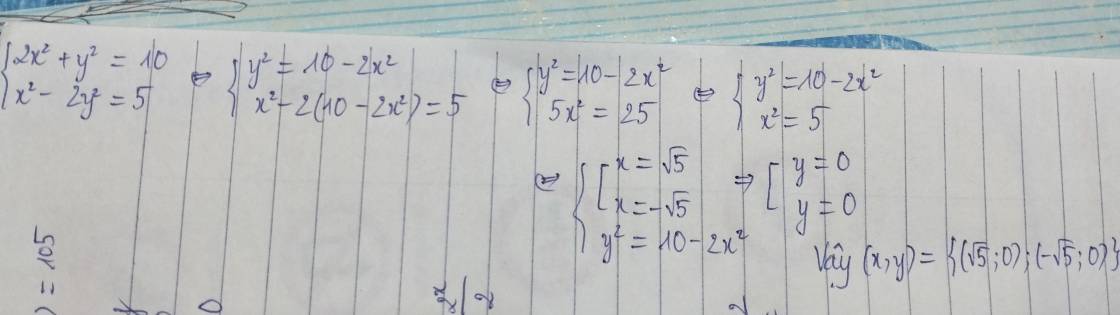\(\left\{{}\begin{matrix}2x^2+y^2=10\\x^2-2y^2=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4x^2+2y^2=20\\x^2-2y^2=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}5x^2=25\\x^2-2y^2=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2=5\\5-2y^2=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x=\sqrt{5}\\x=-\sqrt{5}\end{matrix}\right.\\2y^2=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x=\sqrt{5}\\x=-\sqrt{5}\end{matrix}\right.\\y^2==0\end{matrix}\right.\)
\(\left\{{}\begin{matrix}\left[{}\begin{matrix}x=\sqrt{5}\\x=-\sqrt{5}\end{matrix}\right.\\y=0\end{matrix}\right.\)
Vậy \(S=\left\{\left(-\sqrt{5};0\right);\left(\sqrt{5};0\right)\right\}\)