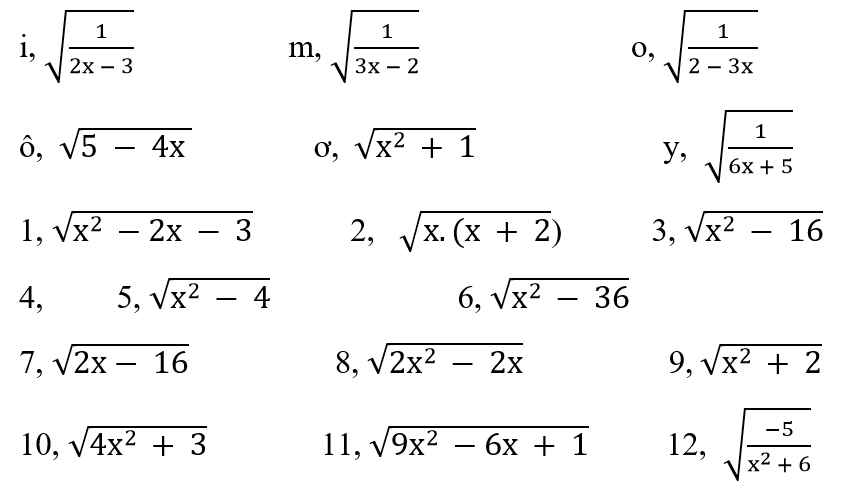1)
a) để biểu thức có nghĩa thì \(x-2\ge0\)
⇔ \(x\ge2\)
vậy để biểu thức có nghĩa thì \(x\ge2\)
b) để biểu thức có nghĩa thì \(3x^2-6x+3\ge0\)
⇔ \(3x^2-3x-3x+3\ge0\)
⇔ \(3x\left(x-1\right)-3\left(x-1\right)\ge0\)
⇔ \(\left(x-1\right)\left(3x-3\right)\ge0\)
⇔ \(3\left(x-1\right)^2\ge0\)
⇔ \(x-1\ge0\)
⇔ \(x\ge1\)
vậy để biểu thức có nghĩa thì \(x\ge1\)
2)
a) \(2\sqrt{x-3+3}=x\)
⇔ \(2\sqrt{x}=x\)
⇔ \(x-2\sqrt{x}=0\)
⇔ \(\sqrt{x}\left(\sqrt{x}-2\right)=0\)
⇔ \(\left[{}\begin{matrix}\sqrt{x}=0\\\sqrt{x}-2=0\end{matrix}\right.\)
⇔ \(\left[{}\begin{matrix}x=0\\x=4\end{matrix}\right.\)
Vậy \(S=\left\{0;4\right\}\)
b) \(2x^2-9=0\)
⇔ \(\left(\sqrt{2}x+3\right)\left(\sqrt{2x}-3\right)=0\)
⇔ \(\left[{}\begin{matrix}\sqrt{2}x+3=0\\\sqrt{2}x-3=0\end{matrix}\right.\)
⇔ \(\left[{}\begin{matrix}x=-\dfrac{3\sqrt{2}}{2}\\x=\dfrac{3\sqrt{2}}{2}\end{matrix}\right.\)
Vậy \(S=\left\{-\dfrac{3\sqrt{2}}{2};\dfrac{3\sqrt{2}}{2}\right\}\)
3)
\(x\sqrt{\dfrac{5y}{x^2}}=\sqrt{x^2.\dfrac{5y}{x^2}}=\sqrt{5y}\)
4)
\(\sqrt{\dfrac{x^2-4x+4}{4}}=\sqrt{\dfrac{\left(x-2\right)^2}{2^2}}=\dfrac{\sqrt{\left(x-2\right)^2}}{\sqrt[]{2^2}}=\dfrac{\left|x-2\right|}{2}\)