Bài 3:
a: \(\sqrt{3x-5}=7\)
\(\Leftrightarrow3x-5=49\)
\(\Leftrightarrow3x=54\)
hay x=18
Bài 3:
b. \(\sqrt{100-200x}-\dfrac{3}{4}\sqrt{16-32x}+2\sqrt{1-2x}=18\)
<=> \(\sqrt{100\left(1-2x\right)}-\dfrac{3}{4}\sqrt{16\left(1-2x\right)}+2\sqrt{1-2x}=18\)
<=> \(10\sqrt{1-2x}-3\sqrt{1-2x}+2\sqrt{1-2x}=18\)
<=> \(\left(10-3+2\right)\sqrt{1-2x}=18\)
<=> \(11\sqrt{1-2x}=18\)
<=> \(\sqrt{1-2x}=\dfrac{18}{11}\)
<=> 1 - 2x = \(\left(\dfrac{18}{11}\right)^2\)
<=> 1 - 2x = \(\dfrac{324}{121}\)
<=> \(1-\dfrac{324}{121}=2x\)
<=> \(2x=\dfrac{-203}{121}\)
<=> \(x=\dfrac{-203}{242}\)
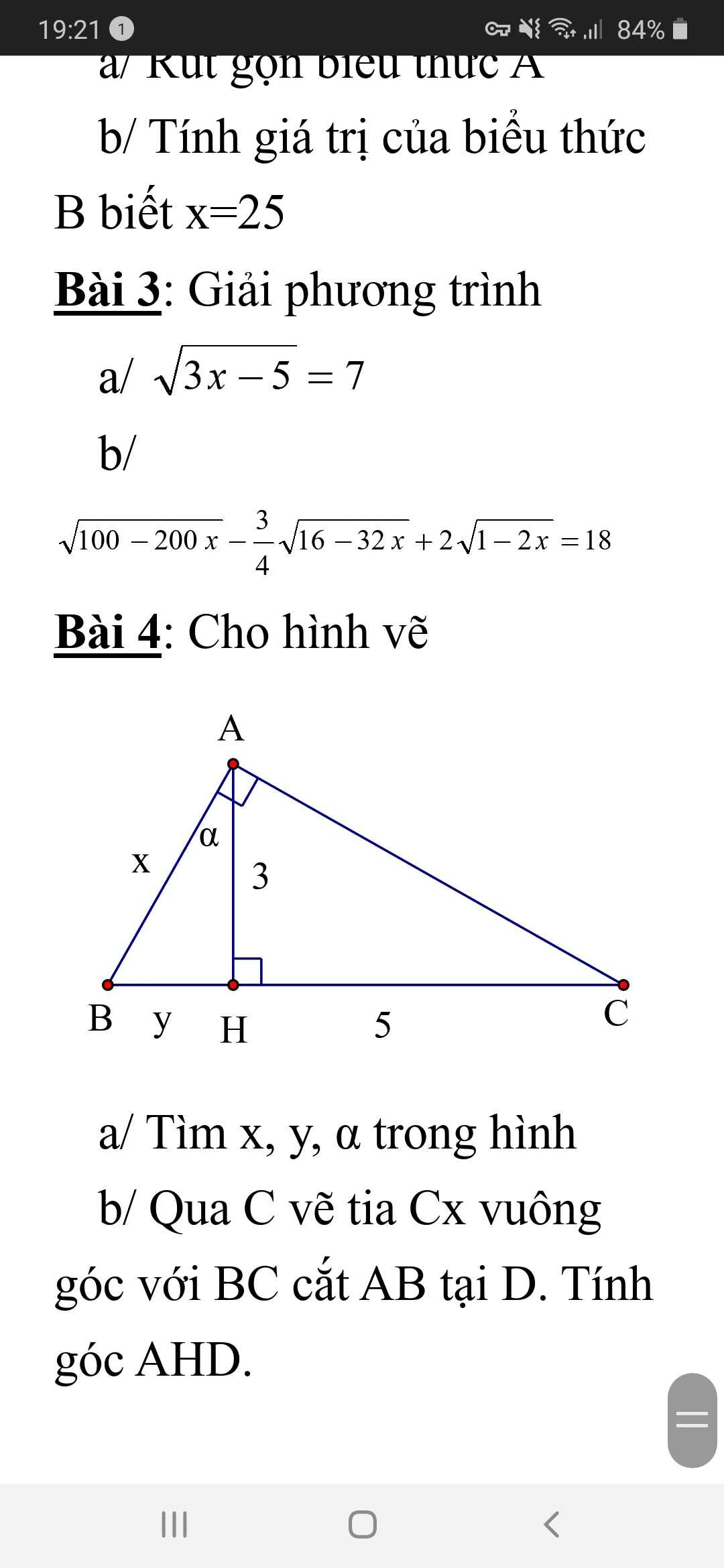
Bài 4:
Áp dụng hệ thức lượng trong tam giác vuông:
$AH^2=BH.CH$
$3^2=y.5\Rightarrow y=\frac{9}{5}=1,8$
Áp dụng định lý Pitago:
$x=\sqrt{3^2+y^2}=\sqrt{9+1,8^2}=\frac{3\sqrt{34}}{5}$
$\tan \alpha = \frac{BH}{AH}=\frac{y}{3}=\frac{1,8}{3}=\frac{3}{5}$
$\Rightarrow \alpha \approx 31^0$
b.
$AH\perp BC, CD\perp BC$ nên $AH\parallel CD$
Áp dụng định lý Talet:
$\frac{AH}{CD}=\frac{BH}{BC}$
$\Rightarrow DC=\frac{AH.BC}{BH}=\frac{3(y+5)}{y}=\frac{3(1,8+5)}{1,8}=\frac{34}{3}$
$\tan \widehat{HDC}=\frac{HC}{CD}=\frac{5}{\frac{34}{3}}=\frac{15}{34}$
$\Rightarrow \widehat{HDC}=23,8^0$
$\widehat{AHD}=\widehat{HDC}=23,8^0$ (hai góc so le trong)
















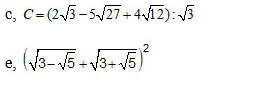
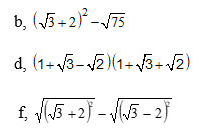 các bạn giải hộ mik mấy câu này vs mik đag cần gấp
các bạn giải hộ mik mấy câu này vs mik đag cần gấp


 bài/2.1/bài dùng chặn
bài/2.1/bài dùng chặn
