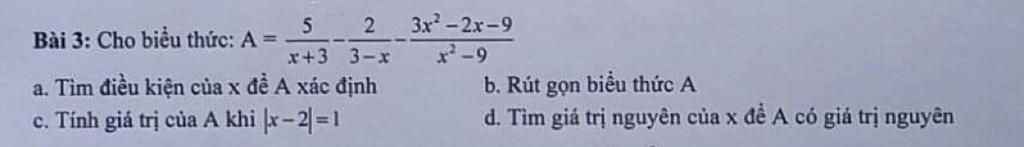\(a;ĐKXĐ:x\ne\pm3\\ A=\left(\dfrac{2x-1}{x+3}+\dfrac{x}{x-3}-\dfrac{3-10x}{x^2-9}\right):\dfrac{x+2}{x-3}\\ =\left[\dfrac{\left(2x-1\right)\left(x-3\right)+x\left(x+3\right)-3+10x}{\left(x-3\right)\left(x+3\right)}\right]\cdot\dfrac{x-3}{x+2}\\ =\left[\dfrac{2x^2-6x-x+3+x^2+3x-3+10x}{\left(x-3\right)\left(x+3\right)}\right]\cdot\dfrac{x-3}{x+2}\\ =\dfrac{3x^2+6x}{\left(x-3\right)\left(x+3\right)}\cdot\dfrac{x-3}{x+2}\\ =\dfrac{3x\left(x+2\right)\left(x-3\right)}{\left(x-3\right)\left(x+3\right)\left(x+2\right)}\\ =\dfrac{3x}{x+3}\)
b; đặt \(\dfrac{3x}{x+3}=y\Rightarrow x=\dfrac{3y}{3-y}\)
đặt 3 - y = k => y = 3 - k
\(\Rightarrow x=\dfrac{3\cdot\left(3-k\right)}{3-\left(3-k\right)}=\dfrac{9-3k}{k}=\dfrac{9}{k}-3\)
\(=>k\inƯ\left(9\right)=\left\{\pm1;\pm3;\pm9\right\}\)
k = 1 => x = 6 (thoả mãn đkxđ)
k = -1 => x = -12 (thoả mãn đkxđ)
k = 3 => x = 0 (thoả mãn đkxđ)
k = -3 => x = -6 (thoả mãn đkxđ)
k = 9 => x = -2 (thoả mãn đkxđ)
k = -9 => x = -4 (thoả mãn đkxđ)
=> \(x\in\left\{;6;-12;0;-6;-2;-4\right\}\) thì A có giá trị nguyên