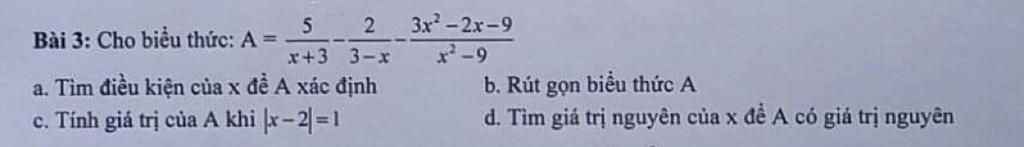\(x^2+y^2-2x+2y+2=0\\ \Leftrightarrow\left(x^2-2x+1\right)+\left(y^2+2y+1\right)=0\\ \Leftrightarrow\left(x-1\right)^2+\left(y+1\right)^2=0\\ \Leftrightarrow\left\{{}\begin{matrix}\left(x-1\right)^2=0\\\left(y+1\right)^2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-1\end{matrix}\right.\)
\(M=\left(x+y\right)^{2018}+\left(x-2\right)^{2019}+\left(y+1\right)^{2020}\\ M=\left(1-1\right)^{2018}+\left(1-2\right)^{2019}+\left(-1+1\right)^{2020}\\ M=0^{2018}+\left(-1\right)^{2019}+0^{2020}=-1\)