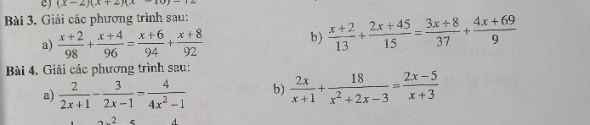\(a,-3x^2+2x+1=0\\ \Leftrightarrow\left(-3x^2-x\right)+\left(3x+1\right)=0\\ \Leftrightarrow-x.\left(3x+1\right)+\left(3x+1\right)=0\\ \Leftrightarrow\left(3x+1\right).\left(1-x\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}1-x=0\\3x+1=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{1}{3}\end{matrix}\right.\\ \Rightarrow S=\left\{-\dfrac{1}{3};1\right\}\\ b,\dfrac{x+1}{x}-\dfrac{x+5}{x-2}=\dfrac{1}{x^2-2x}\left(ĐKXĐ:x\ne0;x\ne2\right)\\ \Leftrightarrow\dfrac{\left(x-2\right).\left(x+1\right)-\left(x+5\right).x}{x.\left(x-2\right)}=\dfrac{1}{\left(x-2\right).x}\\ \Leftrightarrow x^2-2x+x-2-x^2-5x=1\\ \Leftrightarrow-2x+x-5x=1+2\\ \Leftrightarrow-6x=3\\ \Leftrightarrow x=\dfrac{-3}{6}=-\dfrac{1}{2}\left(TM\right)\\ \Rightarrow S=\left\{-\dfrac{1}{2}\right\}\)
