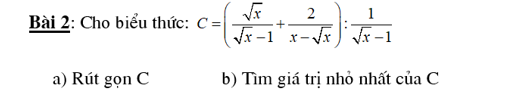c: ĐKXĐ: \(x\notin\left\{3;4;5;6\right\}\)
\(\dfrac{x}{x-3}-\dfrac{x}{x-5}=\dfrac{x}{x-4}-\dfrac{x}{x-6}\)
=>\(\dfrac{x\left(x-5\right)-x\left(x-3\right)}{\left(x-3\right)\left(x-5\right)}=\dfrac{x\left(x-6\right)-x\left(x-4\right)}{\left(x-4\right)\left(x-6\right)}\)
=>\(\dfrac{x^2-5x-x^2+3x}{\left(x-3\right)\left(x-5\right)}=\dfrac{x^2-6x-x^2+4x}{\left(x-4\right)\left(x-6\right)}\)
=>\(-\dfrac{2x}{\left(x-3\right)\left(x-5\right)}=\dfrac{-2x}{\left(x-4\right)\left(x-6\right)}\)
=>\(\dfrac{x}{\left(x-3\right)\left(x-5\right)}-\dfrac{x}{\left(x-4\right)\left(x-6\right)}=0\)
=>\(x\left(\dfrac{1}{\left(x-3\right)\left(x-5\right)}-\dfrac{1}{\left(x-4\right)\left(x-6\right)}\right)=0\)
=>\(\left[{}\begin{matrix}x=0\\\left(x-3\right)\left(x-5\right)=\left(x-4\right)\left(x-6\right)\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=0\\x^2-8x+15=x^2-10x+24\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\2x=9\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=0\left(nhận\right)\\x=\dfrac{9}{2}\left(nhận\right)\end{matrix}\right.\)
`c)x/(x-3)-x/(x-5)=x/(x-4)-x/(x-6)` `(ĐK: x<>3;x<>4;x<>5;x<>6)`
`<=>(x(x-5)-x(x-3))/((x-3)(x-5))=(x(x-6)-x(x-4))/((x-4)(x-6)`
`<=>(-2x)/((x-3)(x-5))=(-2x)/((x-4)(x-6))`
`<=>(x-3)(x-5)=(x-4)(x-6)`
`<=>x^2-3x-5x+15=x^2-4x-6x+24`
`<=>x^2-8x+15=x^2-10x+24`
`<=>-8x+10x=24-15`
`<=>2x=11`
`<=>x=11/2`








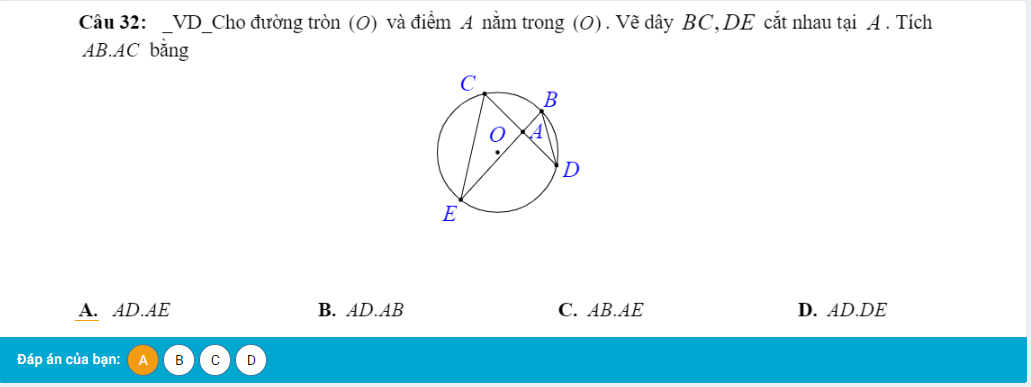

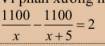


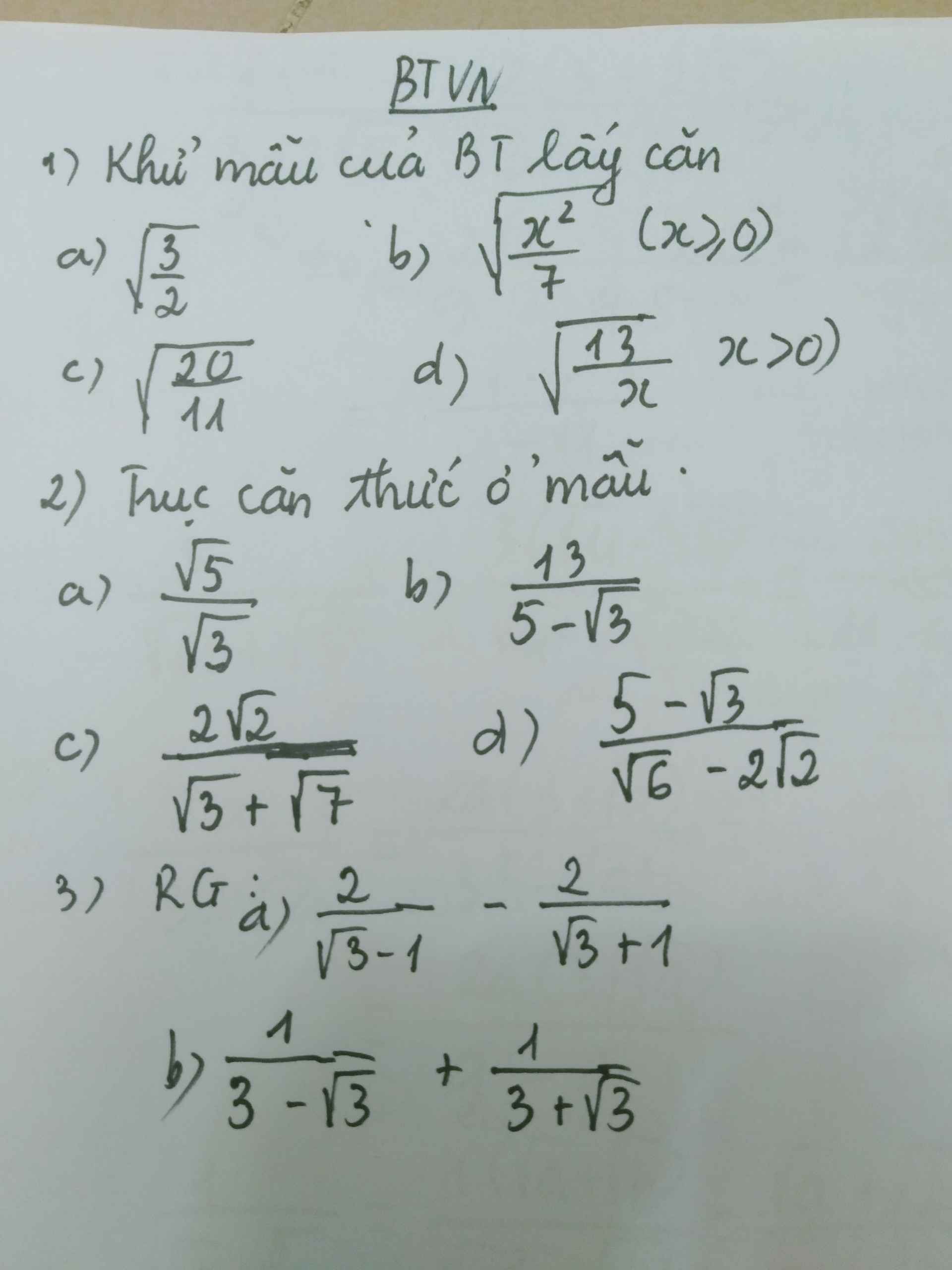


 HELP ME
HELP ME