\(y'=2x-2< 0;\forall x\in\left[-3;-1\right]\)
\(\Rightarrow\) Hàm số nghịch biến trên \(\left[-3;-1\right]\)
\(\Rightarrow\min\limits_{\left[-3;-1\right]}y=y\left(-1\right)=\left(-1\right)^2-2.\left(-1\right)=3\)
GTNN của hàm số y = x 3 + 3 x 2 - 9 x + 1 trên đoạn [-4;4] là
A. -4
B. 1
C. 4
D. -1
Cho hàm số f(x), đồ thị hàm số y=f '(x) là đường cong trong hình bên. Giá trị lớn nhất của hàm số g(x) = -f(2x-1) +2x trên đoạn [0;2] bằng
Giá trị lớn nhất của hàm số y = x - 2 x + 1 trên đoạn là
A. 2
B. - 1 2
C. 1
D. 0
Tìm GTLN (max); GTNN (min) của hàm số y = 2 x + 1 + 4 - x .
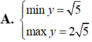
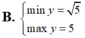
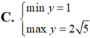
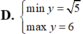
GTNN của hàm số y = x + 2 + 1 ( x - 1 ) trên khoảng (1; +∞) là:
A. Không tồn tại
B. 5
C. 1
D. 2
Cho hàm số y=f(x) là hàm số chẵn, liên tục trên đoạn [-1;1] và thỏa mãn ∫ 0 1 2 f ( x ) d x = 3 , ∫ 1 4 1 2 f ( 2 x ) d x = 1 . Tính I= ∫ - π 2 0 cos x f ( sin x ) d x
Tìm GTLN (max), GTNN (min) của hàm số y = x + 2 x 2 + 1 trên - 1 ; 1
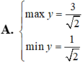
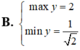
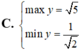
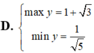
GTLN, GTNN của hàm số
y=x3 _ 3x2 - 9x + 35 trên đoạn [ -4,4] lần lược là
trong các hàm số sau hàm số nào đồng biến trên R: A. y= 2x-1/x+2 B. y= -x^3+x^2-5x C. y= x^3+2x+1 D.-x^4-2x^2+3
Cho hàm số y = x 2 - 2 | x | + 2 và các mệnh đề
(1) Hàm số trên liên tục trên R
(2) Hàm số trên có đạo hàm tại x = 0
(3) Hàm số trên đạt GTNN tại x = 0.
(4) Hàm số trên đạt GTLN tại x = 0.
(5) Hàm số trên là hàm chẵn
(6) Hàm số trên cắt trục hoành tại duy nhất một điểm
Trong các mệnh đề trên, số mệnh đề đúng là
A. 1
B. 2
C. 3
D. 4
