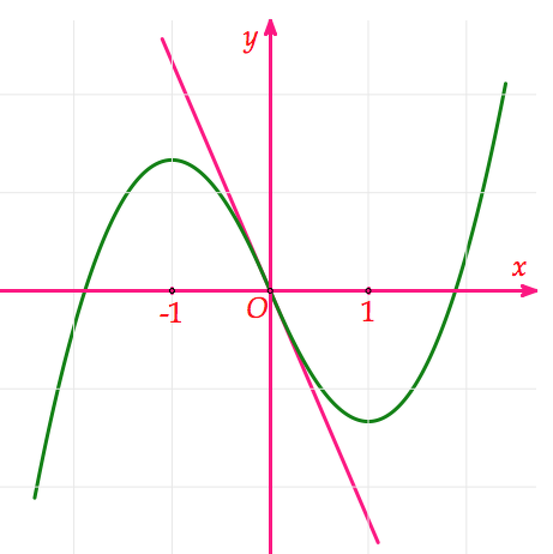
Gọi M là điểm có hoành độ khác 0, thuộc đồ thị (C) của hàm số y = x 3 - 3 x . Tiếp tuyến của (C) tại M cắt (C) tại điểm thứ hai là N (N không trùng với M). Kí hiệu x M , x N thứ tự là hoành độ của M và N. Kết luận nào sau đây là đúng?
A. 2 x M + x N = 0
B. x M + 2 x N = 3
C. x M + x N = - 2
D. x M + x N = 3
Đáp án A
Gọi M x 0 ; y 0 ∈ C ⇒ y ' x 0 = 3 x 0 2 - 3 và y x 0 = x 0 3 - 3 x 0 .
Suy ra phương trình tiếp tuyến của (C) tại M là y = y x 0 = y ' x 0 . x - x 0 .
⇔ y = 3 x 0 2 - 3 . x - x 0 + x 0 3 - 3 x 0 = 3 x 0 2 - 3 . x - 2 x 0 3 ( d ) .
Phương trình hoành độ giao điểm của (C) và (d) là x 3 - 3 x = 3 x 0 2 - 3 x - 2 x 0 3
⇔ x 3 - 3 x 0 2 . x + 2 x 0 3 = 0 ⇔ x - x 0 2 x + 2 x 0 = 0 ⇔ [ x = x 0 x = - 2 x 0 .
Vậy x M = x 0 x N = - 2 x 0 ⇒ 2 x M + x N = 0 .