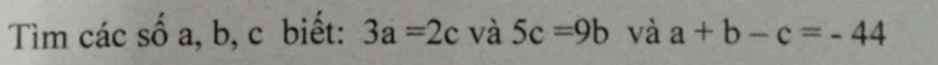Do \(\left\{{}\begin{matrix}0\le\left|a\right|\le1\\0\le\left|b-1\right|\le2\end{matrix}\right.\)
\(\Rightarrow\left|a\right|.\left|b-1\right|\le1.2\)
\(\Rightarrow\left|ab-a\right|\le2\)
Mà \(\left|a-c\right|\le3\Rightarrow\left|ab-a\right|+\left|a-c\right|\le3+2\)
\(\Rightarrow\left|ab-a\right|+\left|a-c\right|\le5\) (1)
Áp dụng BĐT trị tuyệt đối:
\(\left|ab-a\right|+\left|a-c\right|\ge\left|ab-a+a-c\right|=\left|ab-c\right|\) (2)
Từ (1);(2) \(\Rightarrow\left|ab-c\right|\le5\)


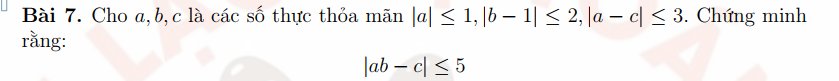







 m
m