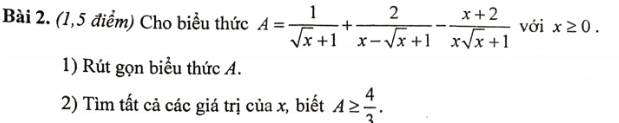a: Xét ΔABC vuông tại A có AH là đường cao
nên \(AH^2=HB\cdot HC\)
=>\(HC\cdot3=6^2=36\)
=>HC=12(cm)
BC=BH+HC
=3+12
=15(cm)
b: Xét tứ giác AHBE có
\(\widehat{AHB}=\widehat{AEB}=\widehat{HBE}=90^0\)
Do đó: AHBE là hình chữ nhật
=>HE=BA
Xét ΔBKC vuông tại B có BA là đường cao
nên \(BA^2=AK\cdot AC\)
=>\(HE^2=AK\cdot AC\)
Xét ΔABK vuông tại A có AE là đường cao
nên \(BE\cdot EK=AE^2\)
\(BH\cdot BC+BE\cdot EK\)
\(=AE^2+AH^2\)
\(=AE^2+EB^2\)
\(=AB^2\)
\(=AK\cdot AC\)
c: Ta có: AHBE là hình chữ nhật
=>\(S_{AHBE}=AH\cdot AE\)
=>\(S_{AHBE}< =AH^2+AE^2=AB^2\)
Dấu '=' xảy ra khi AH=AE
Hình chữ nhật AHBE có AH=AE
nên AHBE là hình vuông
=>BA là phân giác của \(\widehat{HBE}\)
=>\(\widehat{ABC}=45^0\)
Xét ΔABC vuông tại A có \(\widehat{ABC}=45^0\)
nên ΔABC vuông cân tại A
Ta có: ΔABC vuông cân tại A
mà AH là đường cao
nên H là trung điểm của BC
giải hộ mk vs chỉ cần có cách làm câu b thôi câu a thì ko cần
