a,
\(AH^2=x^2=BH.HC\\ x^2=4.9\\ x^2=36\\ x=6\left(cm\right)\)
b,
\(AC=tanB.AB=>AB=\dfrac{AC}{tanB}=\dfrac{5}{tan50}\)
c, \(6^2=3.x\\ x=36:3\\ x=12\\ y^2=12.\left(12+3\right)\\y^2=12.15\\ y^2=180\\ y=6\sqrt{5}\)
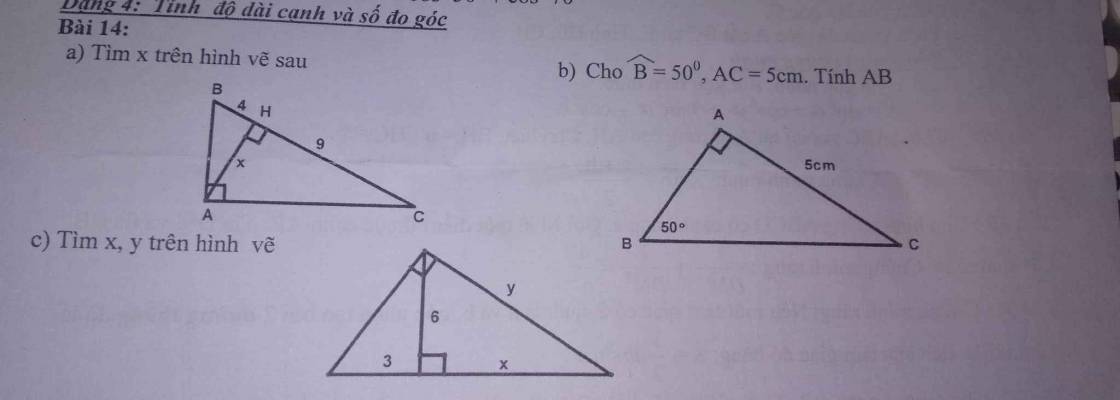
a) Tam giác ABC vuông tại A, đường cao AH
Suy ra AH² = BH.HC (hệ thức lượng trong tam giác vuông)
AH² = 4 . 9 = 36
AH = 6
Vậy x = 6
b) Tam giác ABC vuông tại A
Suy ra tanB = AC : AB
Suy ra AB = AC : tanB
= 5 : tan50⁰ ~ 4,2
c) Ta có: 6² = 3 . x
x = 36 : 3 = 12
y² = 12² + 6² (Pytago)
= 180
y = 6 căn 5