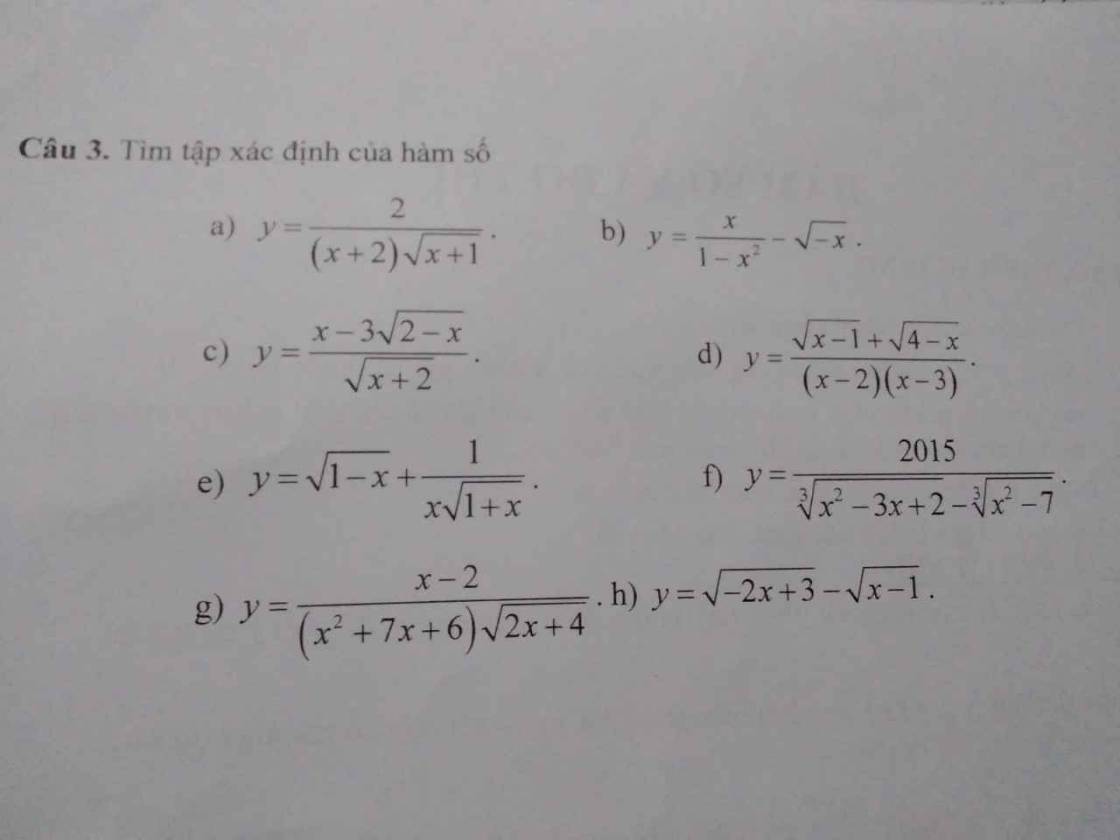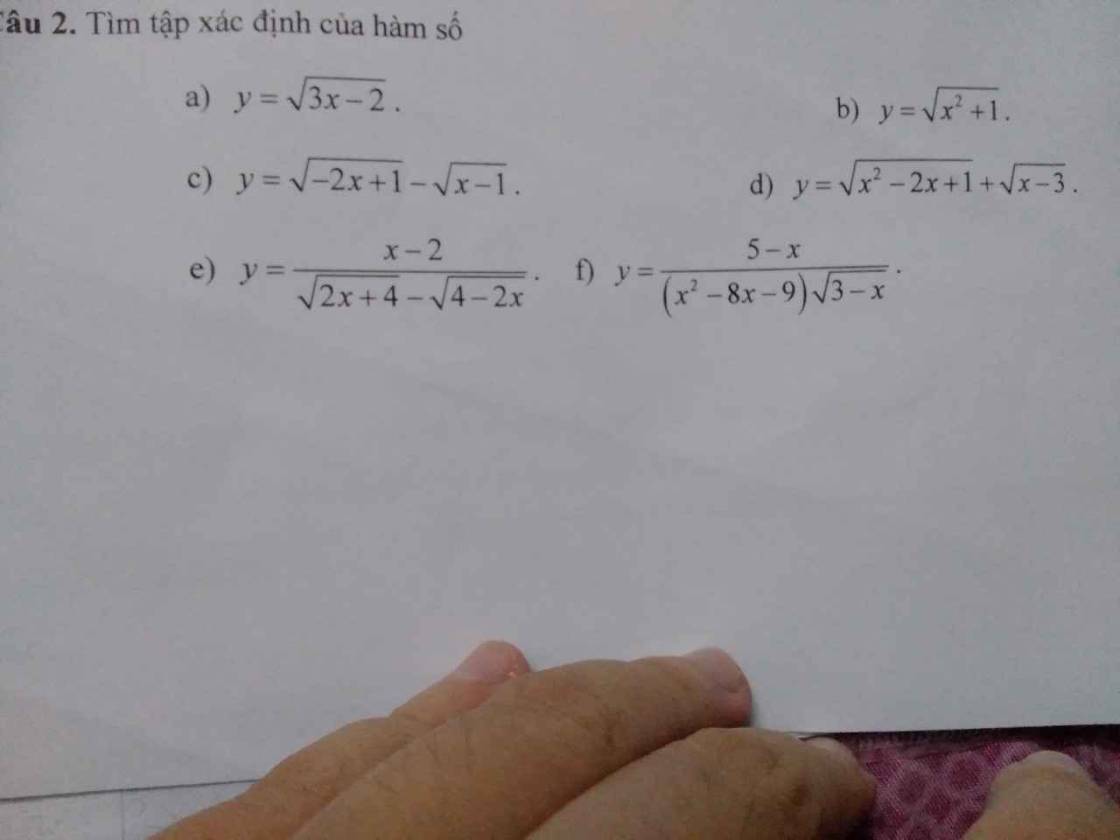Bài 2:
\(a,3x-2\ge0\Leftrightarrow x\ge\dfrac{2}{3}\\ b,x^2+1>0\forall x\\ c,\left\{{}\begin{matrix}-2x+1\ge0\\x-1\ge0\end{matrix}\right.\Leftrightarrow1\le x\le\dfrac{1}{2}\left(loại\right)\Rightarrow x\in\varnothing\)
Bài 2:
\(d,\left\{{}\begin{matrix}x^2-2x+1\ge0\\x-3\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(x-1\right)^2\ge0\left(đúng\right)\\x\ge3\end{matrix}\right.\Rightarrow x\ge3\\ e,\left\{{}\begin{matrix}2x+4\ge0\\4-2x\ge0\\\sqrt{2x+4}\ne\sqrt{4-2x}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ge-2\\x\le2\\2x+4\ne4-2x\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}-2\le x\le2\\x\ne0\end{matrix}\right.\)
\(f,\left\{{}\begin{matrix}x^2-8x-9\ne0\\3-x>0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x\ne9\\x\ne-1\\x< 3\end{matrix}\right.\)
Bài 3:
\(a,\left\{{}\begin{matrix}x\ne-2\\x>-1\end{matrix}\right.\\ b,\left\{{}\begin{matrix}1-x^2\ne0\\-x\ge0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x\ne-1\\x\le0\end{matrix}\right.\\ c,\left\{{}\begin{matrix}2-x\ge0\\x+2>0\end{matrix}\right.\Rightarrow-2< x\le2\\ d,\left\{{}\begin{matrix}x\ne2\\x\ne3\\x-1\ge0\\4-x\ge0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x\ne2\\x\ne3\\1\le x\le4\end{matrix}\right.\)
Bài 3:
\(e,\left\{{}\begin{matrix}1-x\ge0\\1+x>0\\x\ne0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}-1< x\le1\\x\ne0\end{matrix}\right.\\ f,x^2-3x+2\ne x^2-7\Leftrightarrow3x\ne9\Leftrightarrow x\ne3\\ g,\left\{{}\begin{matrix}x^2+7x+6\ne0\\2x+4>0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x\ne-1\\x\ne-6\\x>-2\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x>-2\\x\ne-1\end{matrix}\right.\\ h,\left\{{}\begin{matrix}-2x+3\ge0\\x-1\ge0\end{matrix}\right.\Rightarrow1\le x\le\dfrac{3}{2}\)
Câu 2.
(a) Hàm số xác định khi \(3x-2\ge0\Leftrightarrow x\ge\dfrac{3}{2}\)
\(\Rightarrow D=[\dfrac{3}{2};+\infty)\)
(b) Hàm số xác định khi: \(x^2+1\ge0\) (luôn đúng).
\(\Rightarrow D=R.\)
(c) Hàm số xác định khi: \(\left\{{}\begin{matrix}-2x+1\ge0\\x-1\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\le\dfrac{1}{2}\\x\ge1\end{matrix}\right.\) (vô lí) \(\Rightarrow D=\varnothing\).
(d) Hàm số xác định khi: \(\left\{{}\begin{matrix}x^2-2x+1\ge0\\x-3\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(x-1\right)^2\ge0\left(LĐ\right)\\x\ge3\end{matrix}\right.\)
\(\Rightarrow D=[3;+\infty)\)
(e) Hàm số xác địn
h khi: \(\left\{{}\begin{matrix}2x+4\ge0\\4-2x\ge0\\2x+4\ne4-2x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ge-2\\x\le2\\x\ne0\end{matrix}\right.\)
=> D = [-2; 2] \ {0}.
(f) Hàm số xác định khi: (Sửa lại dấu ngoặc nhọn hết nhé):\(\left\{{}\begin{matrix}3-x\ge0\\\left[{}\begin{matrix}x^2-8x-9\ne0\\3-x\ne0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\le3\\\left[{}\begin{matrix}\left\{{}\begin{matrix}x\ne-1\\x\ne9\end{matrix}\right.\\x\ne3\end{matrix}\right.\end{matrix}\right.\)
=> D = (-∞; 3) \ {-1}.