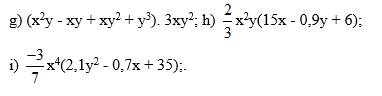\(g,\left(x^2y-xy+xy^2+y^3\right).3xy^2\\ =\left(3xy^2.x^2y\right)-\left(3xy^2.xy\right)+\left(3xy^2.xy^2\right)+\left(3xy^2.y^3\right)\\ =3x^3y^3-3x^2y^3+3x^2y^4+3xy^5\)
\(h,\dfrac{2}{3}x^2y\left(15x-0,9y+6\right)\\ =\left(\dfrac{2}{3}x^2y.15x\right)-\left(\dfrac{2}{3}x^2y.0,9y\right)+\left(\dfrac{2}{3}x^2y.6\right)\\ =10x^3y-\dfrac{3}{5}x^2y^2+4x^2y\)
\(i,-\dfrac{3}{7}x^4\left(2,1y^2-0,7x+35\right)\\ =\left(-\dfrac{3}{7}x^4.2,1y^2\right)-\left(-\dfrac{3}{7}x^4.0,7x\right)+\left(-\dfrac{3}{7}x^4.35\right)\\ =-\dfrac{9}{10}x^4y^2+\dfrac{3}{10}x^5-15x^4\)
g: =x^2y*3xy^2-xy*3xy^2+xy^2*3xy^2+y^3*3xy^2
=3x^3y^3-3x^2y^3+3x^2y^4+3xy^5
h: =2/3x^2y*15x-2/3x^2y*0,9y+2/3x^2y*6
=10x^3y-0,6x^2y^2+4x^2y
i: =-3/7x^4*2,1y^2+3/7x^4*0,7x-3/7x^4*35
=-0,9x^4y^2+3/10x^5-15x^4
g)(x2y-xy+xy2+y3).3xy2
=x2y.3xy2 - xy.3xy2+ xy2.3xy2 + y3.3xy2
= 3x3y3 - 3x2y3 + 3x2y4 +3xy5
h)2/3x2y(15x-0,9y+6)
=2/3x2y.15x - 2/3x2y.0,9y + 2/3x2y.6
= 10x3y - 3/5x2y2 + 4x2y
i)-3/7x4(2,1y2-0,7x+35)
= -3/7x4.2,1y2 + 3/7x4.0,7x - 3/7x4.35
= -9/10x4y2 + 3/10x5 - 15x4