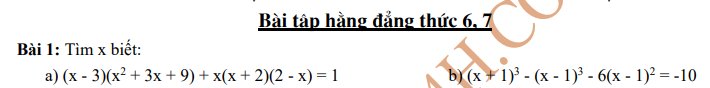a) \(\left(x-3\right)\left(x^2+3x+9\right)-x\left(x+2\right)\left(2-x\right)=1\)
\(\Leftrightarrow\left(x-3\right)\left(x^2+3x+9\right)+x\left(x+2\right)\left(x-2\right)=1\)
\(\Leftrightarrow\left(x^3-3^3\right)-x\left(x+2\right)\left(x-2\right)=1\)
\(\Leftrightarrow x^3-27-x\left(x^2-2^2\right)=1\)
\(\Leftrightarrow x^3-27-x^3+4x=1\)
\(\Leftrightarrow4x-27=1\)
\(\Leftrightarrow4x=28\)
\(\Leftrightarrow x=7\)
b) \(\left(x+1\right)^3-\left(x-1\right)^3-6\left(x-1\right)^2=-10\)
\(\Leftrightarrow\left[\left(x+1\right)-\left(x-1\right)\right]\left[\left(x+1\right)^2+\left(x-1\right)\left(x+1\right)+\left(x-1\right)^2\right]-6\left(x-1\right)^2=-10\)
\(\Leftrightarrow2\left[\left(x+1\right)^2+\left(x^2-1\right)+\left(x-1\right)^2\right]-6\left(x-1\right)^2=-10\)
\(\Leftrightarrow2\left[\left(x^2+2x+1\right)+\left(x^2-1\right)+\left(x^2-2x+1\right)\right]-6\left(x-1\right)^2=-10\)
\(\Leftrightarrow2\left(x^2+2x+1+x^2-1+x^2-2x+1\right)-6\left(x-1\right)^2=-10\)
\(\Leftrightarrow2\left(3x^2+1\right)-6\left(x-1\right)^2=-10\)
\(\Leftrightarrow6x^2+2-6\left(x^2-2x+1\right)=-10\)
\(\Leftrightarrow6x^2+2-6x^2+12x-6=-10\)
\(\Leftrightarrow12x-4=-10\)
\(\Leftrightarrow12x=-6\)
\(\Leftrightarrow x=-\dfrac{6}{12}=-\dfrac{1}{2}\)
\(a,\left(x-3\right)\left(x^2+3x+9\right)+x\left(x+2\right)\left(2-x\right)=1\\ \Leftrightarrow x^3-3x^2+3x^2-9x+9x-27+\left(x^2+2x\right)\left(2-x\right)-1=0\\ \Leftrightarrow x^3-3x^2+3x^2-9x+9x-27+2x^2-x^3+4x-2x^2-1=0\\ \Leftrightarrow x^3-x^3-3x^2+3x^2+2x^2-2x^2-9x+9x+4x=1+27\\ \Leftrightarrow4x=28\\ \Leftrightarrow x=7\)
\(b,\left(x+1\right)^3-\left(x-1\right)^3-6\left(x-1\right)^2=-10\\ \Leftrightarrow\left[\left(x+1\right)-\left(x-1\right)\right].\left[\left(x+1\right)^2+\left(x+1\right)\left(x-1\right)+\left(x-1\right)^2\right]-6\left(x^2-2x+1\right)=-10\\ \Leftrightarrow2.\left[\left(x^2+2x+1\right)+\left(x^2-1\right)+\left(x^2-2x+1\right)\right]-6x^2+12x-6=-10\\ \Leftrightarrow2.\left(3x^2+1\right)-6x^2+12x-6=-10\\ \Leftrightarrow6x^2-6x^2+12x=-10+6-2\\ \Leftrightarrow12x=-6\\ \Leftrightarrow x=-\dfrac{1}{2}\)