a.
ĐKXĐ: \(x\ge-1\)
\(\Leftrightarrow\left(x+1-4\sqrt{x+1}+4\right)+\left(2x+3-6\sqrt{2x+3}+9\right)=0\)
\(\Leftrightarrow\left(\sqrt{x+1}-2\right)^2+\left(\sqrt{2x+3}-3\right)^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}\sqrt{x+1}-2=0\\\sqrt{2x+3}-3=0\end{matrix}\right.\)
\(\Leftrightarrow x=3\)
b.
Ta có:
\(VT=\sqrt{2-x}+\sqrt{7+x}\ge\sqrt{2-x+7+x}=3\)
\(VP=-\left(x-2\right)^2+3\le3\)
Đẳng thức xảy ra khi và chỉ khi:
\(\left\{{}\begin{matrix}\left(2-x\right)\left(7+x\right)=0\\x-2=0\end{matrix}\right.\) \(\Leftrightarrow x=2\)

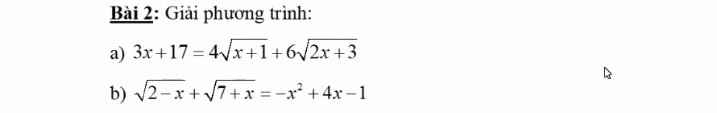




 giúp mình vs mình đg cần gấp
giúp mình vs mình đg cần gấp