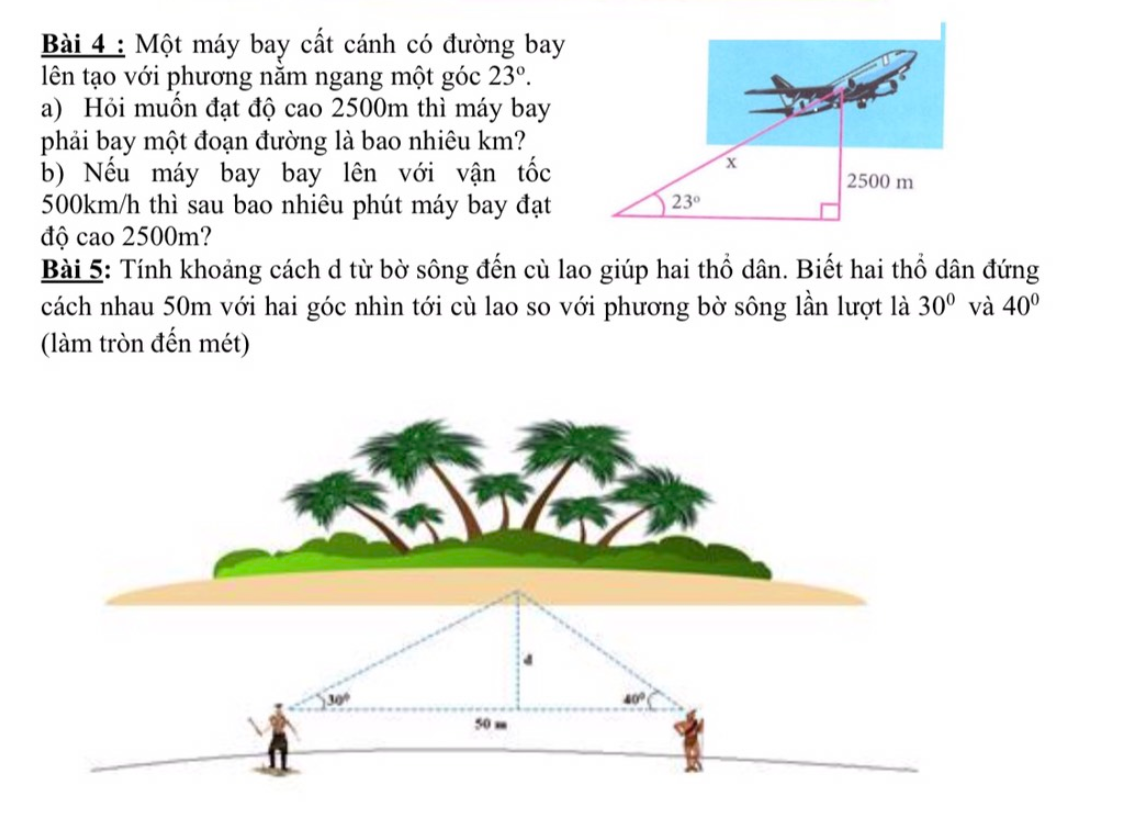
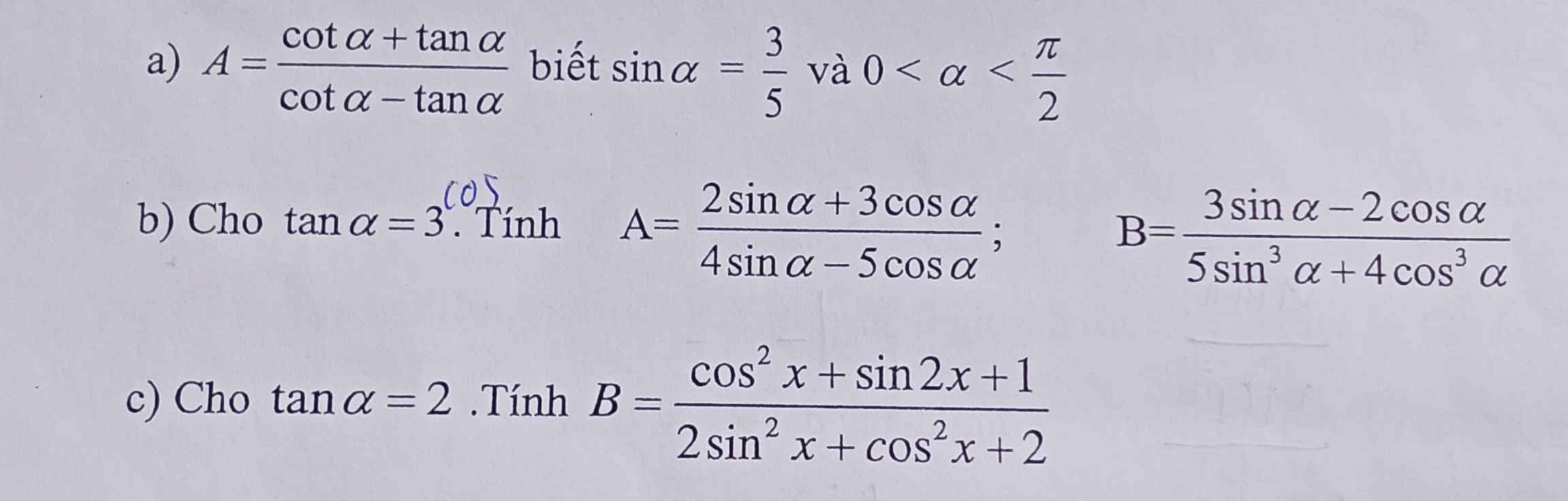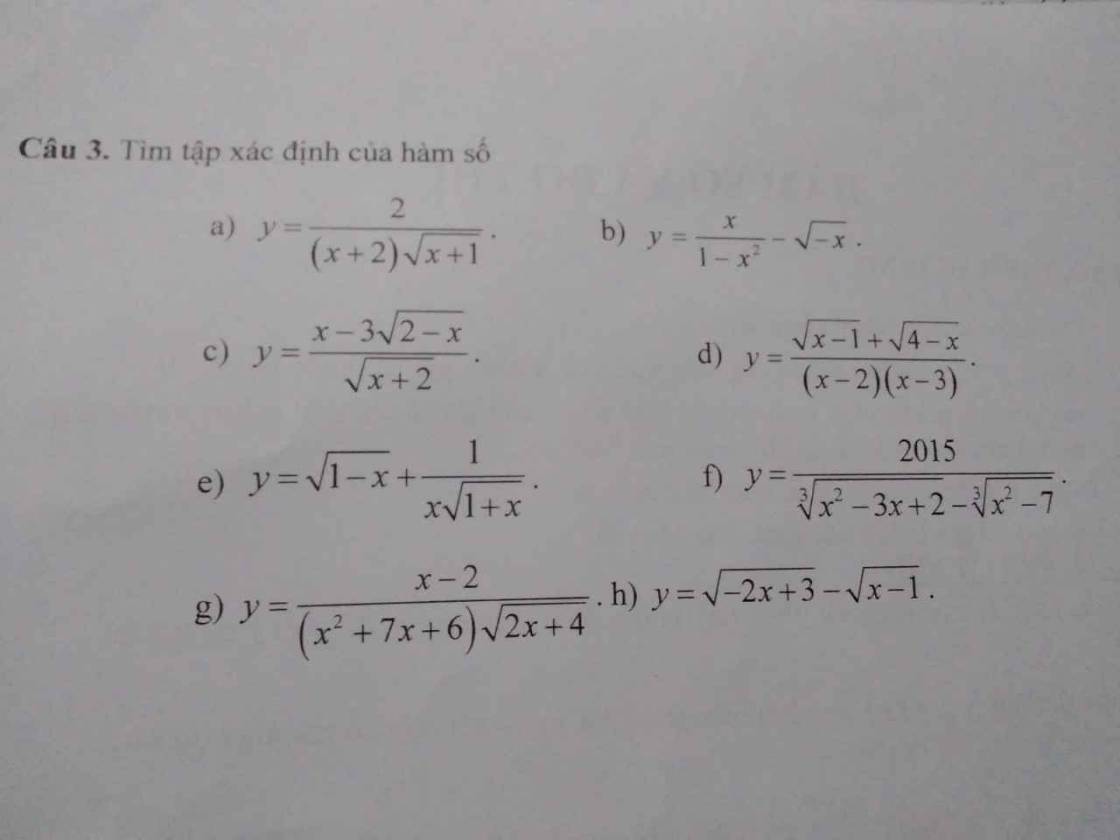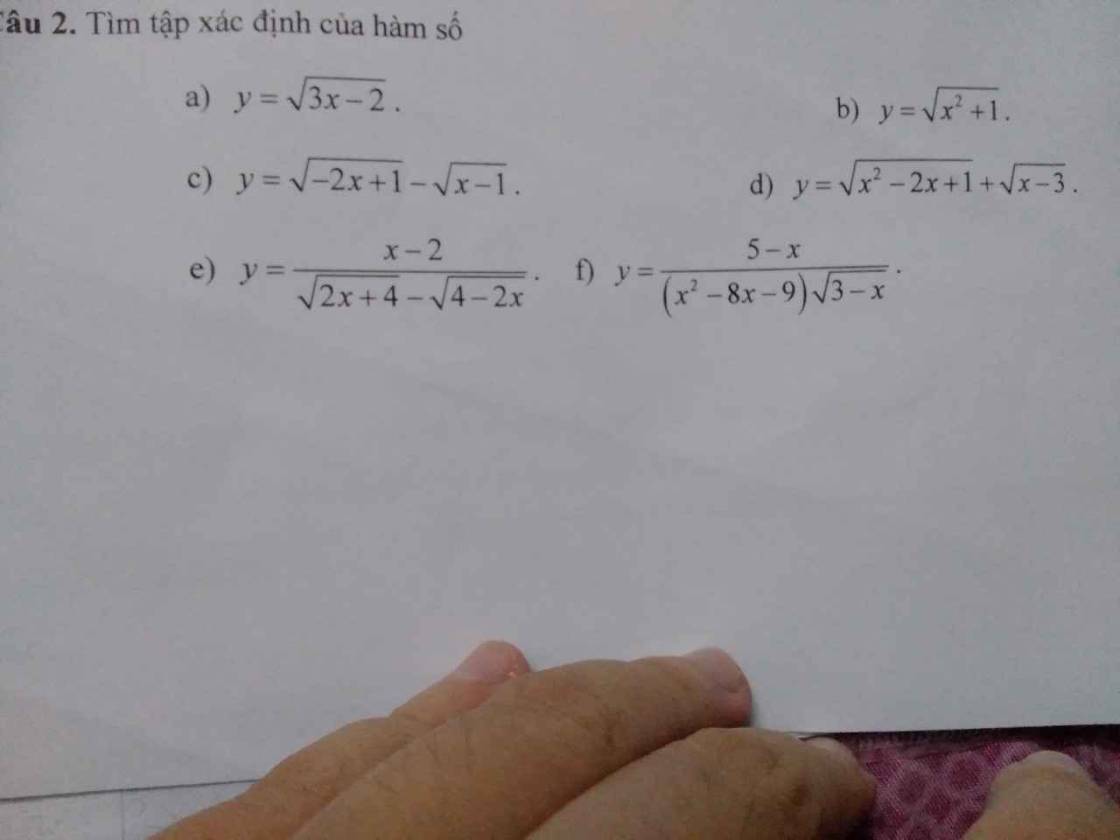a: Xét ΔABC vuông tại A có \(\tan ACB=\dfrac{AB}{AC}\)
=>\(\dfrac{AB}{6}=tan30=\dfrac{\sqrt{3}}{3}\)
=>\(AB=\dfrac{6\sqrt{3}}{3}=2\sqrt{3}\)(cm)
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC=\sqrt{6^2+\left(2\sqrt{3}\right)^2}=\sqrt{36+12}=4\sqrt{3}\left(cm\right)\)
b: Xét ΔAHC vuông tại H có \(sinC=\dfrac{AH}{AC}\)
=>\(\dfrac{AH}{6}=sin30=\dfrac{1}{2}\)
=>AH=3(cm)
c: Xét ΔABC vuông tại A có AM là đường trung tuyến
nên \(AM=\dfrac{BC}{2}=\dfrac{4\sqrt{3}}{2}=2\sqrt{3}\left(cm\right)\)