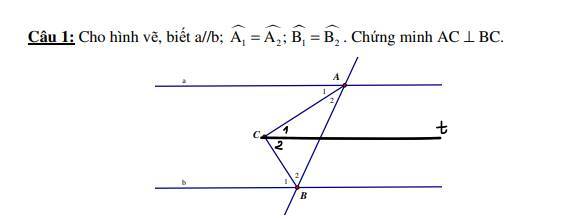
Kẻ `Ct////a`
`=>hat(A_1)=hat(C_1)`(Soletrong)
mà `hat(A_1)=hat(A_2)`
Nên `hat(C_1)=hat(A_2)`
Có `Ct////a`(cách vẽ)
mà `a////b`
Nên `Ct////b`
`=>hat(C_2)=hat(B_1)`(Soletrong)
mà `hat(B_1)=hat(B_2)`
Nên `hat(C_2)=hat(B_2)`
+,Có `a////b(g t)`
`=>hat(A_1)+hat(A_2)+hat(B_1)+hat(B_2)=180^0` (trong cùng phía)
hay `2hat(C_1)+2hat(C_2)=180^0`
`=>2(hat(C_1)+hat(C_2)=180^0`
`=>hat(C_1)+hat(C_2)=90^0`
`=>hat(ACB)=90^0`
`=>AC⊥BC`
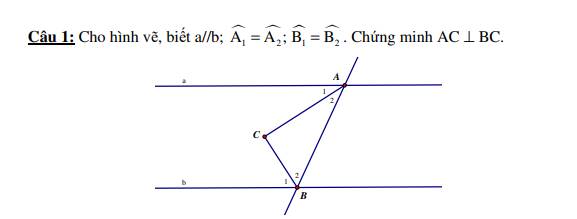
a//b
=>\(\widehat{aAB}+\widehat{ABb}=180^0\)(hai góc trong cùng phía)
=>\(2\cdot\widehat{A_2}+2\cdot\widehat{B_2}=180^0\)
=>\(\widehat{A_2}+\widehat{B_2}=\dfrac{180^0}{2}=90^0\)
=>ΔCAB vuông tại C
=>CA\(\perp\)CB
Do a // b (gt)
\(\Rightarrow\widehat{aAB}=\widehat{ABy}\) (so le trong)
Mà \(\widehat{bBA}+\widehat{ABy}=180^0\) (kề bù)
\(\Rightarrow\widehat{bBA}+\widehat{aAB}=180^0\)
\(\Rightarrow\widehat{B_1}+\widehat{B_2}+\widehat{A_1}+\widehat{A_2}=180^0\)
Mà \(\widehat{A_1}=\widehat{A_2};\widehat{B_1}=\widehat{B_2}\)
\(\Rightarrow2\widehat{A_1}+2\widehat{B_1}=180^0\)
\(\Rightarrow\widehat{A_1}+\widehat{B_1}=180^0:2=90^0\)
Qua C, vẽ tia Cz // a // b
Do Cz // a
\(\Rightarrow\widehat{ACz}=\widehat{A_1}\) (so le trong)
Do Cz // b
\(\widehat{BCz}=\widehat{B_1}\) (so le trong)
\(\Rightarrow\widehat{ACB}=\widehat{ACz}+\widehat{BCz}\)
\(=\widehat{A_1}+\widehat{B_1}=90^0\)
\(\Rightarrow AC\perp BC\)
giúp mình với mn ơi mình cần giúp khẩn cấp T_T
giúp mình với ạ,mình xin cảm ơn trước