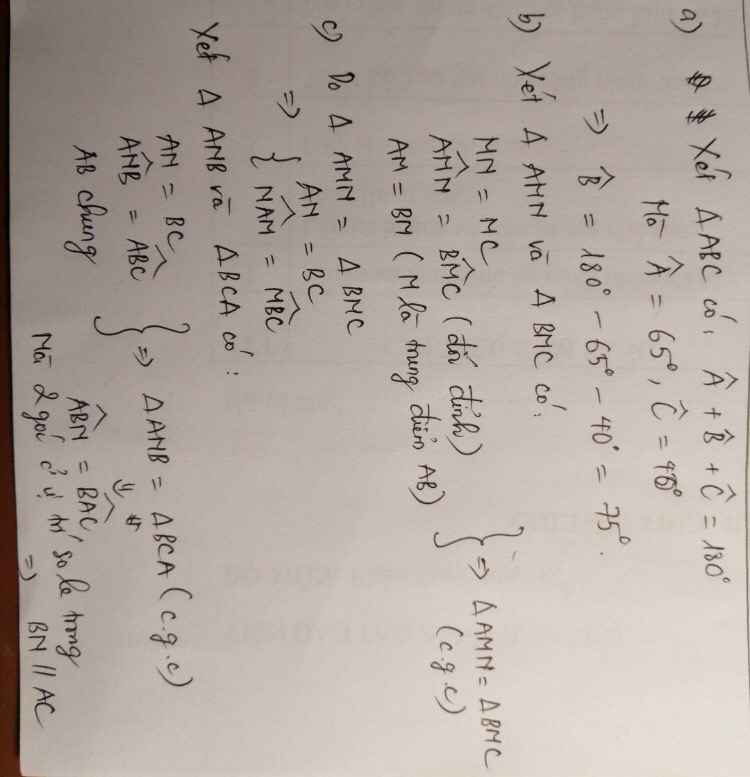a: \(\widehat{B}=180^0-65^0-40^0=75^0\)
b: Xét ΔAMN và ΔBMC có
MA=MB
\(\widehat{AMN}=\widehat{BMC}\)
MN=MC
Do đó: ΔAMN=ΔBMC
c: Xét tứ giác ANBC có
M là trung điểm của AB
M là trung điểm của NC
Do đó: ANBC là hình bình hành
Suy ra: AC//BN
a: ˆB=1800−650−400=750B^=1800−650−400=750
b: Xét ΔAMN và ΔBMC có
MA=MB
ˆAMN=ˆBMCAMN^=BMC^
MN=MC
Do đó: ΔAMN=ΔBMC
c: Xét tứ giác ANBC có
M là trung điểm của AB
a: ˆB=1800−650−400=750B^=1800−650−400=750
b: Xét ΔAMN và ΔBMC có
MA=MB
ˆAMN=ˆBMCAMN^=BMC^
MN=MC
Do đó: ΔAMN=ΔBMC
c: Xét tứ giác ANBC có
M là trung điểm của AB