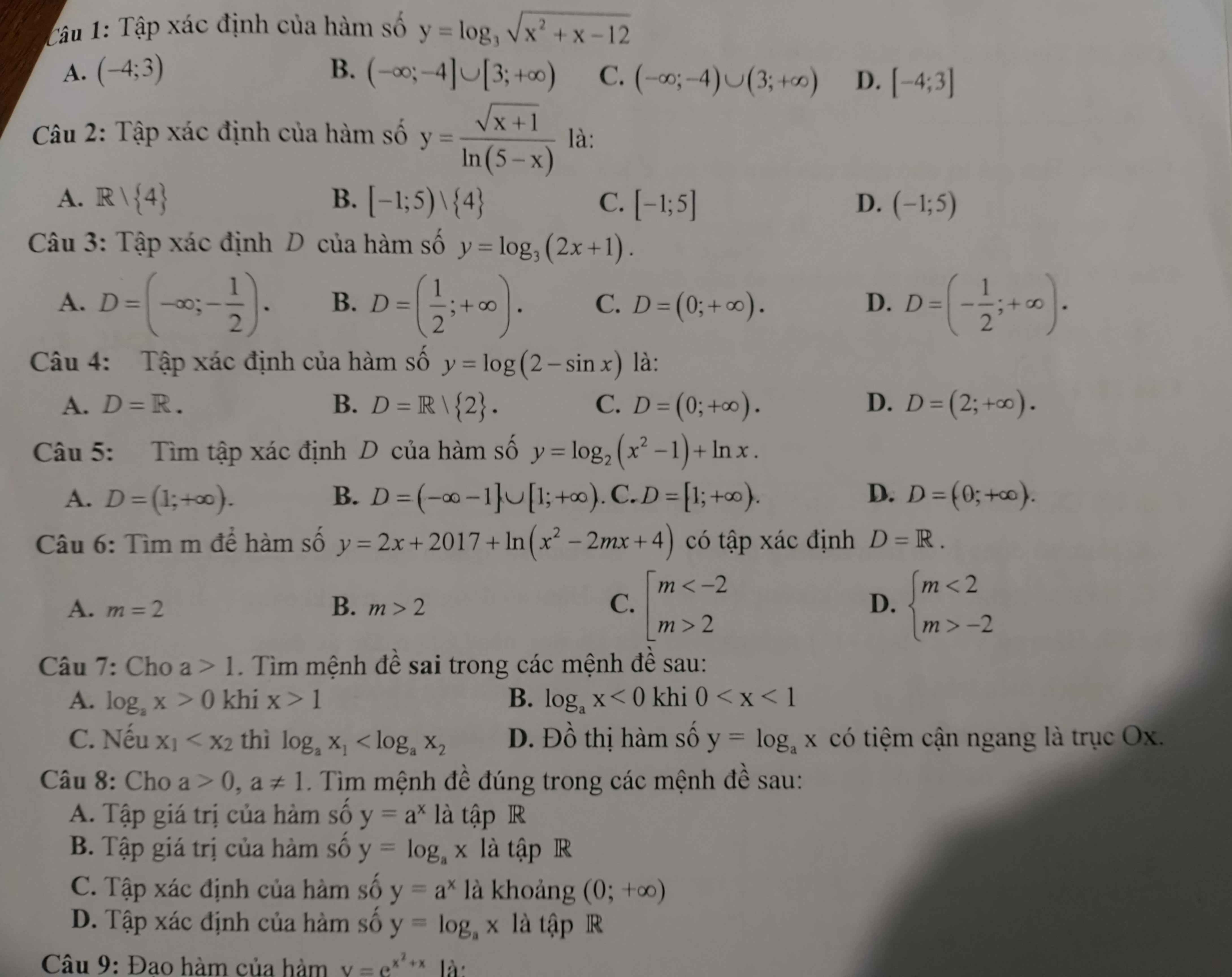Câu 1:
ĐKXĐ: $x^2+x-12>0$
$\Leftrightarrow (x-3)(x+4)>0$
$\Leftrightarrow x>3$ hoặc $x<-4$
$\Leftrightarrow x\in (3;+\infty)\cup (-\infty; -4)$
Đáp án C.
Câu 2:
ĐKXĐ: \(\left\{\begin{matrix} x+1\geq 0\\ 5-x>0\\ 5-x\neq 1\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq -1\\ x< 5\\ x\neq 4\end{matrix}\right.\Leftrightarrow x\in [-1;5)\setminus \left\{4\right\}\)
Đáp án B.
Câu 3:
ĐKXĐ: $2x+1>0$
$\Leftrightarrow x> \frac{-1}{2}$
$\Leftrightarrow x\in (\frac{-1}{2}; +\infty)$
Đáp án D.
Câu 4:
ĐKXĐ: $2-\sin x>0$
$\Leftrightarrow \sin x< 2$ (điều này luôn đúng vì $\sin x\in [-1;1], \forall x\in\mathbb{R}$)
Vậy TXĐ $x\in\mathbb{R}$
Đáp án A.
Câu 5:
ĐKXĐ: \(\left\{\begin{matrix} x^2-1>0\\ x>0\end{matrix}\right.\left\{\begin{matrix} (x-1)(x+1)>0\\ x>0\end{matrix}\right.\Leftrightarrow x-1>0\Leftrightarrow x>1\Leftrightarrow x\in (1;+\infty)\)
Đáp án A.
Câu 6:
Để hàm số có TXĐ $D=\mathbb{R}$ thì $x^2-2mx+4>0, \forall x\in\mathbb{R}$
$\Leftrightarrow \Delta'=m^2-4<0$
$\Leftrightarrow (m-2)(m+2)<0\Leftrightarrow -2< m< 2$
$\Leftrightarrow m\in (-2;2)$
Đáp án D.
Câu 7:
C. Thiếu điều kiện $x_1,x_2>0$
D. Sai, vì \(\lim\limits_{x\to +\infty}\log_ax\neq 0\)
Câu 8:
A. Sai, vì $y=a^x>0$ với mọi $a>0$
B. Đúng
C. Sai. $x$ có thể nhận giá trị thực bất kỳ
D. Sai. $x\in (0;+\infty)$
Câu 9:
$y'=(e^{x^2+x})'=(x^2+x)'e^{x^2+x}=(2x+1)e^{x^2+x}$
Đáp án A.
Câu 10:
$y'=(2x-1)'3^x+(2x-1)(3^x)'=2.3^x+(2x-1)\ln 3.3^x$
$=3^x(2+2x\ln 3-\ln 3)$
Đáp án B.
Câu 11:
\(y'=[\log_2(x+e^x)]'=\frac{(x+e^x)'}{(x+e^x)\ln 2}=\frac{1+e^x}{(x+e^x).\ln 2}\)
Đáp án D>
Câu 12:
\(f'(x)=[\log_5(x^2+x+1)]'=\frac{(x^2+x+1)'}{(x^2+x+1)\ln 5}=\frac{2x+1}{(x^2+x+1)\ln 5}\)
Đáp án A
Câu 13:
\(y'=x'e^x+x(e^x)'=e^x+xe^x\)
\(y''=(e^x+xe^x)'=(e^x+y)'=(e^x)'+y'=e^x+e^x+xe^x=2e^x+xe^x\)
\(=2(e^x+xe^x)-xe^x=2y'-y\)
$\Rightarrow y''-2y'+y=0$
Đáp án C.
Câu 14:
$x\in [-2;2]\Rightarrow |x|\in [0;2]$
$\Rightarrow y=2^{|x|}\in [2^0; 2^2]$ hay $y\in [1;4]$
Vậy $y_{\min}=1; y_{\max}=4$