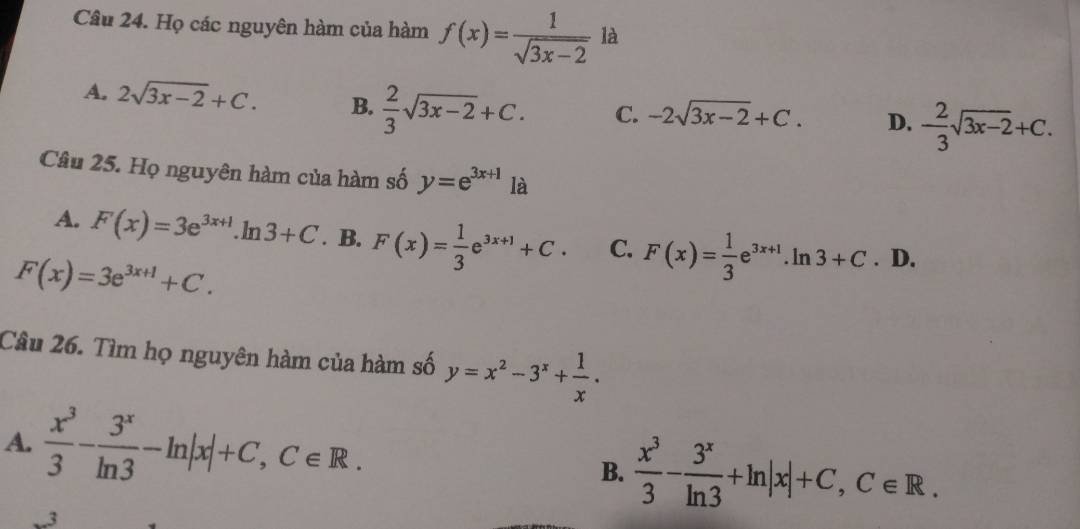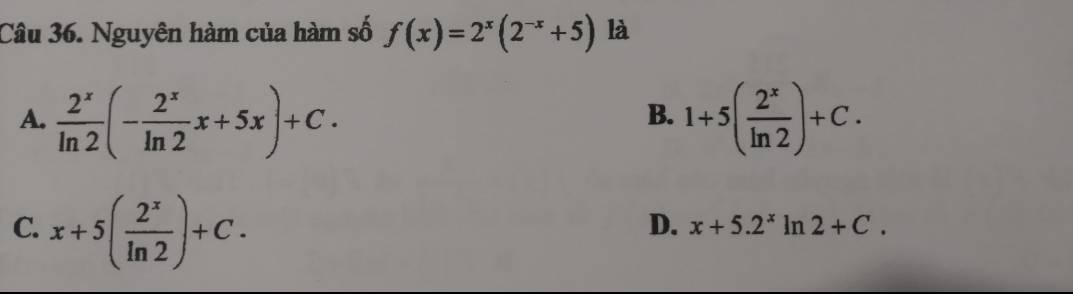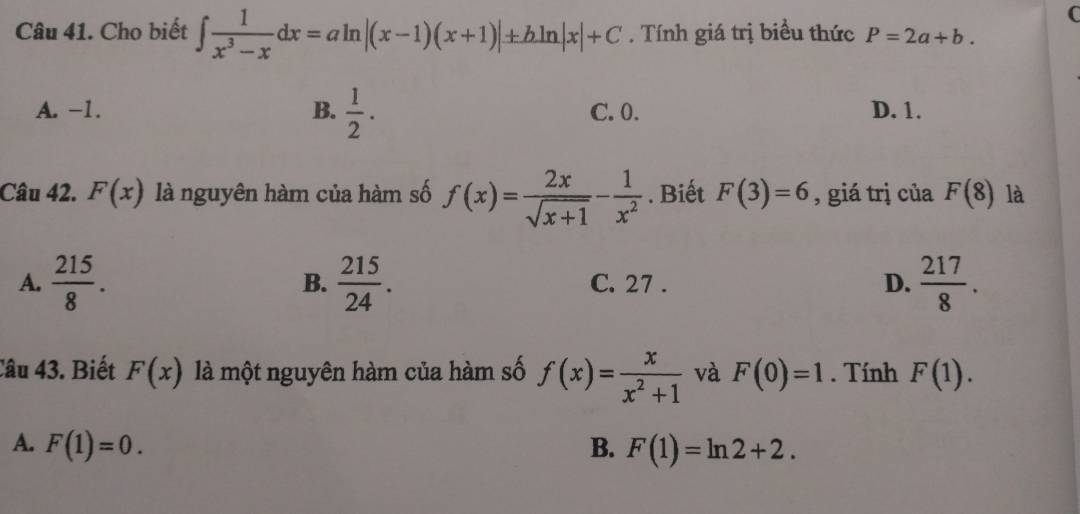27.
Bán kính mặt cầu ngoại tiếp tứ diện vuông được tính bằng:
\(R=\sqrt{\dfrac{OA^2+OB^2+OC^2}{4}}=\sqrt{\dfrac{1^2+2^2+3^2}{4}}=\dfrac{\sqrt{14}}{2}\)
28.
Từ giả thiết suy ra \(A\left(2;2;2\right)\)
Gọi điểm thuộc mặt Oxz có tọa độ dạng \(D\left(x;0;z\right)\)
\(\Rightarrow\overrightarrow{AD}=\left(x-2;-2;z-2\right)\)
\(\overrightarrow{BD}=\left(x+2;-2;z\right)\) ; \(\overrightarrow{CD}=\left(x-4;-1;z+1\right)\)
D cách đều A, B, C \(\Rightarrow\left\{{}\begin{matrix}AD=BD\\AD=CD\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\left(x-2\right)^2+4+\left(z-2\right)^2=\left(x+2\right)^2+4+z^2\\\left(x-2\right)^2+4+\left(z-2\right)^2=\left(x-4\right)^2+1+\left(z+1\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x+z=1\\2x-3z=3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}z=-\dfrac{1}{2}\\x=\dfrac{3}{4}\end{matrix}\right.\)
\(\Rightarrow P\left(\dfrac{3}{4};0;-\dfrac{1}{2}\right)\)
29.
Do tâm I mặt cầu thuộc Oz nên tọa độ có dạng: \(I\left(0;0;z\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AI}=\left(-3;1;z-2\right)\\\overrightarrow{BI}=\left(-1;-1;z+2\right)\end{matrix}\right.\)
Mặt cầu qua A, B nên \(AI=BI\)
\(\Leftrightarrow3^2+1^2+\left(z-2\right)^2=1^2+1^2+\left(z+2\right)^2\)
\(\Leftrightarrow8z=8\Rightarrow z=1\)
\(\Rightarrow I\left(0;0;1\right)\Rightarrow R=IB=\sqrt{1^2+1^1+3^2}=\sqrt{11}\)
Phương trình mặt cầu:
\(x^2+y^2+\left(z-1\right)^2=11\)
30.
Từ phương trình mặt cầu ta có:
\(R=\sqrt{1^2+\left(-2\right)^2+2^2-\left(-m\right)}=\sqrt{m+9}\)
\(\Rightarrow\sqrt{m+9}=5\Rightarrow m=16\)
31.
Khoảng cách giữa điểm M và điểm đối xứng với nó qua Ox là \(2\sqrt{y_M^2+z_M^2}=2\sqrt{65}\)
32.
Gọi \(I\left(x;y;z\right)\) là tâm mặt cầu
\(\overrightarrow{AI}=\left(x-1;y;z\right)\) ; \(\overrightarrow{BI}=\left(x;y-1;z\right)\) ; \(\overrightarrow{CI}=\left(x;y;z+1\right)\); \(\overrightarrow{DI}=\left(x-1;y;z-3\right)\)
Do I là tâm mặt cầu
\(\Rightarrow\left\{{}\begin{matrix}AI=BI\\AI=CI\\AI=DI\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\left(x-1\right)^2+y^2+z^2=x^2+\left(y-1\right)^2+z^2\\\left(x-1\right)^2+y^2+z^2=x^2+y^2+\left(z-1\right)^2\\\left(x-1\right)^2+y^2+z^2=\left(x-1\right)^2+y^2+\left(z-3\right)^2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}-x+y=0\\-x+z=0\\-6z+9=0\end{matrix}\right.\) \(\Rightarrow x=y=z=\dfrac{3}{2}\)
Hay \(I\left(\dfrac{3}{2};\dfrac{3}{2};\dfrac{3}{2}\right)\) \(\Rightarrow D\) đúng
33.
Do I thuộc tia Ox nên tọa độ có dạng \(I\left(x;0;0\right)\Rightarrow\overrightarrow{AI}=\left(x-1;2;-3\right)\) với \(x>0\)
\(AI=R\Leftrightarrow\left(x-1\right)^2+2^2+\left(-3\right)^2=49\)
\(\Rightarrow\left(x-1\right)^2=36\Rightarrow\left[{}\begin{matrix}x=7\\x=-5\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow\) Mặt cầu có pt: \(\left(x-7\right)^2+y^2+z^2=49\)
34.
\(cos\left(\overrightarrow{u};\overrightarrow{v}\right)=\dfrac{\overrightarrow{u}.\overrightarrow{v}}{\left|\overrightarrow{u}\right|.\left|\overrightarrow{v}\right|}=\dfrac{1+0-2m}{\sqrt{6}.\sqrt{m^2+1}}=cos45^0=\dfrac{1}{\sqrt{2}}\)
\(\Rightarrow\left\{{}\begin{matrix}m< \dfrac{1}{2}\\2\left(1-2m\right)^2=6\left(m^2+1\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< \dfrac{1}{2}\\m^2-4m-2=0\end{matrix}\right.\)
\(\Rightarrow m=2-\sqrt{6}\)
35.
Do M thuộc Oxy nên tọa độ có dạng: \(M\left(x;y;0\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{MA}=\left(3-x;5-y;-1\right)\\\overrightarrow{MB}=\left(1-x;1-y;3\right)\end{matrix}\right.\)
\(\Rightarrow\overrightarrow{MA}+\overrightarrow{MB}=\left(4-2x;6-2y;2\right)\)
\(\Rightarrow\left|\overrightarrow{MA}+\overrightarrow{MB}\right|=\sqrt{\left(4-2x\right)^2+\left(6-2y\right)^2+2^2}\ge2\)
Dấu "=" xảy ra khi \(\left\{{}\begin{matrix}4-2x=0\\6-2y=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=2\\y=3\\\end{matrix}\right.\)
\(\Rightarrow M\left(2;3;0\right)\)