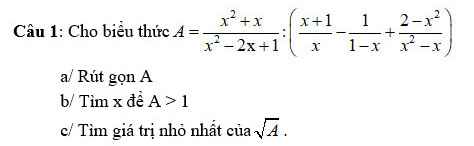a: \(A=\dfrac{x\left(x+1\right)}{\left(x-1\right)^2}:\left(\dfrac{x+1}{x}+\dfrac{1}{x-1}+\dfrac{2-x^2}{x\left(x-1\right)}\right)\)
\(=\dfrac{x\left(x+1\right)}{\left(x-1\right)^2}:\dfrac{x^2-1+x+2-x^2}{x\left(x-1\right)}\)
\(=\dfrac{x\left(x+1\right)}{\left(x-1\right)^2}\cdot\dfrac{x\left(x-1\right)}{x+1}=\dfrac{x^2}{x-1}\)
b: Để A>1 thì A-1>0
\(\Leftrightarrow\dfrac{x^2-x+1}{x-1}>0\)
=>x-1>0
hay x>1
c. \(\sqrt{A}=\sqrt{\dfrac{x^2}{x-1}}=\dfrac{x}{\sqrt{x-1}}=\dfrac{x-1+1}{\sqrt{x-1}}=\dfrac{\left(\sqrt{x-1}\right)^2+1}{\sqrt{x-1}}=\sqrt{x-1}+\dfrac{1}{\sqrt{x-1}}\ge^{Caushy}2\sqrt{\left(\sqrt{x-1}\right).\dfrac{1}{\sqrt{x-1}}}=2\)Dấu "=" xảy ra \(\Leftrightarrow\sqrt{x-1}=\dfrac{1}{\sqrt{x-1}};x\ge1\Leftrightarrow x=2\)
Vậy \(Min\sqrt{A}=2\) khi \(x=2\).