Đặt \(B\left(x\right)=0\)
\(\Rightarrow-1\dfrac{1}{3}x^2+x=0\)
\(\Rightarrow x\left(-1\dfrac{1}{3}+1\right)=0\)
\(\Rightarrow\dfrac{-1}{3}x=0\)
\(\Leftrightarrow x=0\)
Vậy \(x=0\) là nghiệm
\(B(x) = -1\dfrac{1}{3}x^2 + x\)
\(= x( -1\dfrac{1}{3}x + 1 )\)
\(= x( \dfrac{-4}{3}x + 1 )\)
Xét \(B(x) = 0\)
\(=> x( \dfrac{-4}{3}x + 1 ) = 0\)
\(=> \left[\begin{matrix} x = 0 \\ \dfrac{-4}{3}x+1=0\end{matrix}\right.\)
\(=> \left[\begin{matrix} x=0\\ \dfrac{-4}{3}x=-1\end{matrix}\right.\)
\(=> \left[\begin{matrix} x=0\\ x=\dfrac{3}{4}\end{matrix}\right.\)
Vậy \(x \in \) { \( 0 ; \dfrac{3}{4}\) } là nghiệm của B(x) .
\(\text{Đặt B(x)=0}\)
\(\Rightarrow-1\dfrac{1}{3}x^2+x\)
\(\Rightarrow x\left(-1\dfrac{1}{3}x+1\right)=0\)
\(\Rightarrow x\left(-\dfrac{4}{3}x+1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\\dfrac{-4}{3}x+1=0\Rightarrow\dfrac{-4}{3}0-1=-1\Rightarrow x=\left(-1\right):\left(-\dfrac{4}{3}\right)=\dfrac{3}{4}\end{matrix}\right.\)
\(\text{Vậy đa thức B(x) có 2 nghiệm là x=0;x=}\dfrac{3}{4}\)

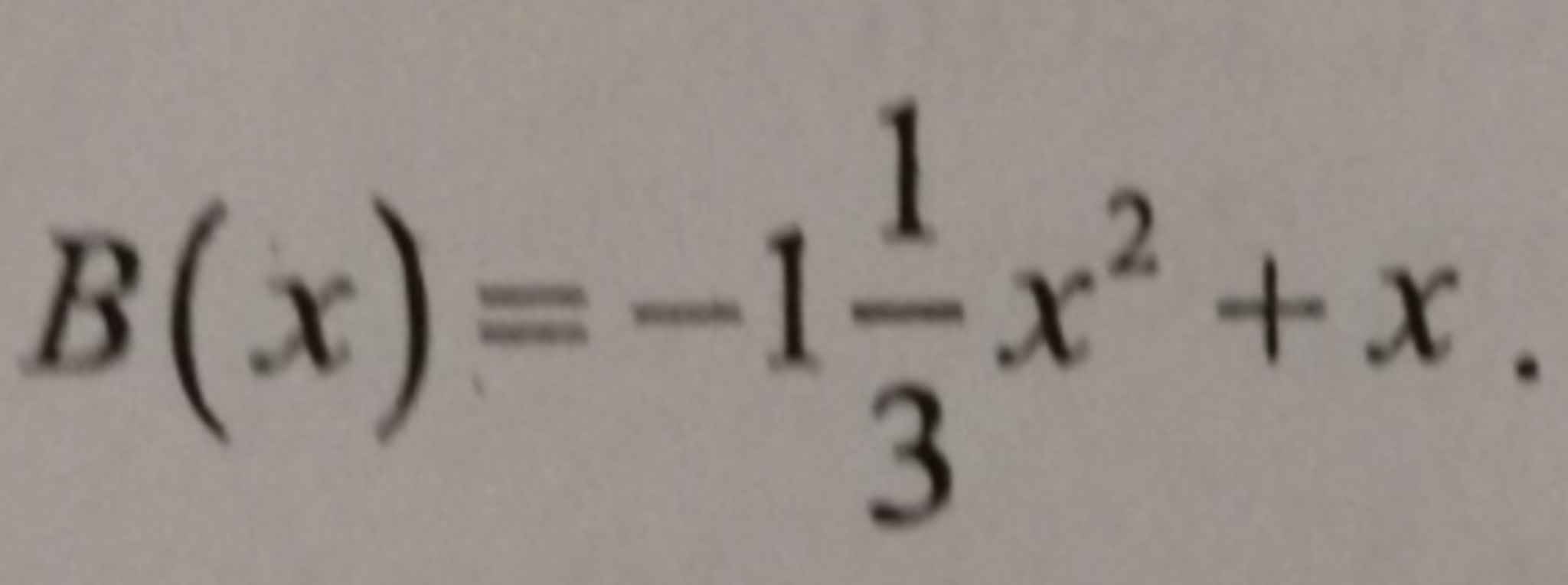














 Các bạn giúp mình phần trắc nghiệm và tự luận nhé . Trắc nghiệm có một số câu ko đúng . Giúp mình nha
Các bạn giúp mình phần trắc nghiệm và tự luận nhé . Trắc nghiệm có một số câu ko đúng . Giúp mình nha