Ta có: \(5\sqrt{\dfrac{9x-27}{25}}-7\sqrt{\dfrac{4x-12}{9}}-7\sqrt{x^2-9}+18\sqrt{\dfrac{9x^2-81}{81}}=0\)
\(\Leftrightarrow5\cdot\dfrac{3\sqrt{x-3}}{5}-7\cdot\dfrac{2\sqrt{x-3}}{7}-7\cdot\sqrt{x^2-9}+18\cdot\dfrac{\sqrt{x^2-9}}{3}=0\)
\(\Leftrightarrow\sqrt{x-3}-\sqrt{x^2-9}=0\)
\(\Leftrightarrow\sqrt{x-3}\left(1-\sqrt{x+3}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\x+3=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\left(nhận\right)\\x=-2\left(loại\right)\end{matrix}\right.\)
ĐK: \(x\ge3\)
\(5\sqrt{\dfrac{9x-27}{25}}-7\sqrt{\dfrac{4x-12}{9}}-7\sqrt{x^2-9}+18\sqrt{\dfrac{9x^2-81}{81}}=0\)
\(\Leftrightarrow3\sqrt{x-3}-\dfrac{14}{3}\sqrt{x-3}-7\sqrt{x^2-9}+6\sqrt{x^2-9}=0\)
\(\Leftrightarrow-5\sqrt{x-3}-3\sqrt{x^2-9}=0\)
Ta thấy \(-5\sqrt{x-3}-3\sqrt{x^2-9}\le0\forall x\ge3\) nên phương trình tương đương:
\(\left\{{}\begin{matrix}\sqrt{x-3}=0\\\sqrt{x^2-9}=0\end{matrix}\right.\)
\(\Leftrightarrow x=3\left(tm\right)\)

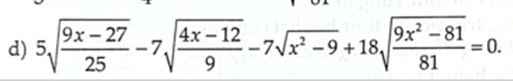






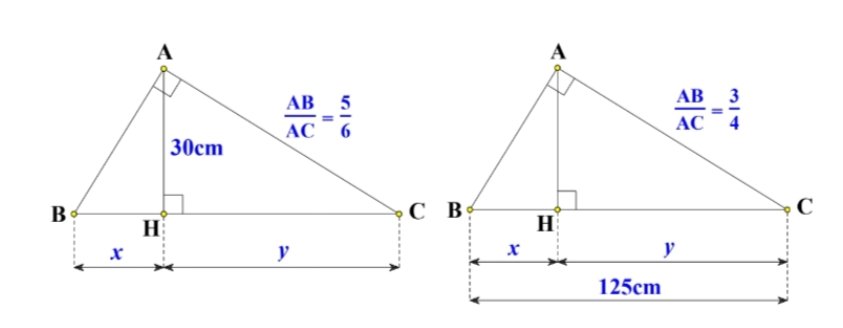

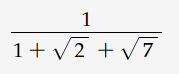 giúp mình câu này với
giúp mình câu này với
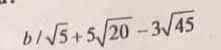




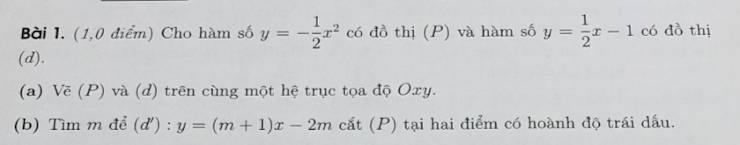 giúp mình câu này với ạ
giúp mình câu này với ạ
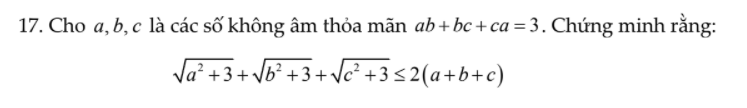 câu này với ạ! Mình cảm ơn.
câu này với ạ! Mình cảm ơn.

