ĐKXĐ: \(x\in R\)
Đặt \(\sqrt{x^2-3x+3}=t>0\)
\(\Rightarrow x^2-3x+6=t^2+3\)
Pt trở thành:
\(t+\sqrt{t^2+3}=3\)
\(\Leftrightarrow\sqrt{t^2+3}=3-t\)
\(\Leftrightarrow\left\{{}\begin{matrix}3-t\ge0\\t^2+3=\left(3-t\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}t\le3\\t^2+3=t^2-6t+9\end{matrix}\right.\)
\(\Rightarrow t=1\)
\(\Rightarrow\sqrt{x^2-3x+3}=1\)
\(\Leftrightarrow x^2-3x+2=0\Rightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)
Đúng 5
Bình luận (0)

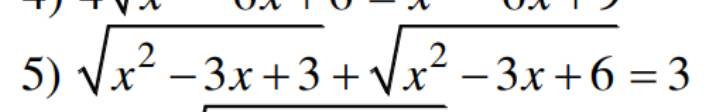








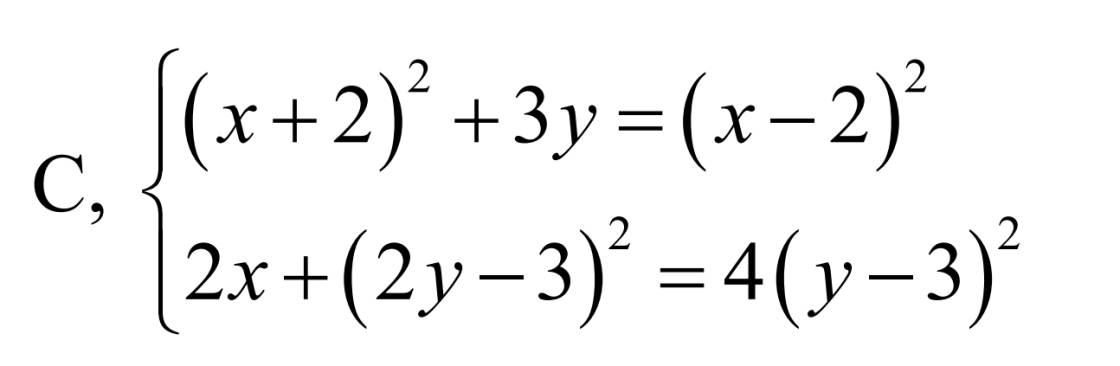




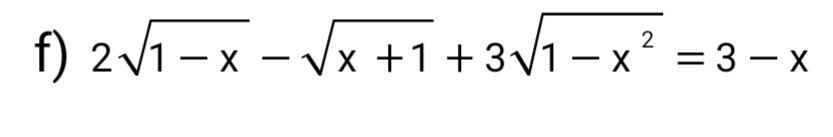 Giải pt . Mn giúp mik vs
Giải pt . Mn giúp mik vs

