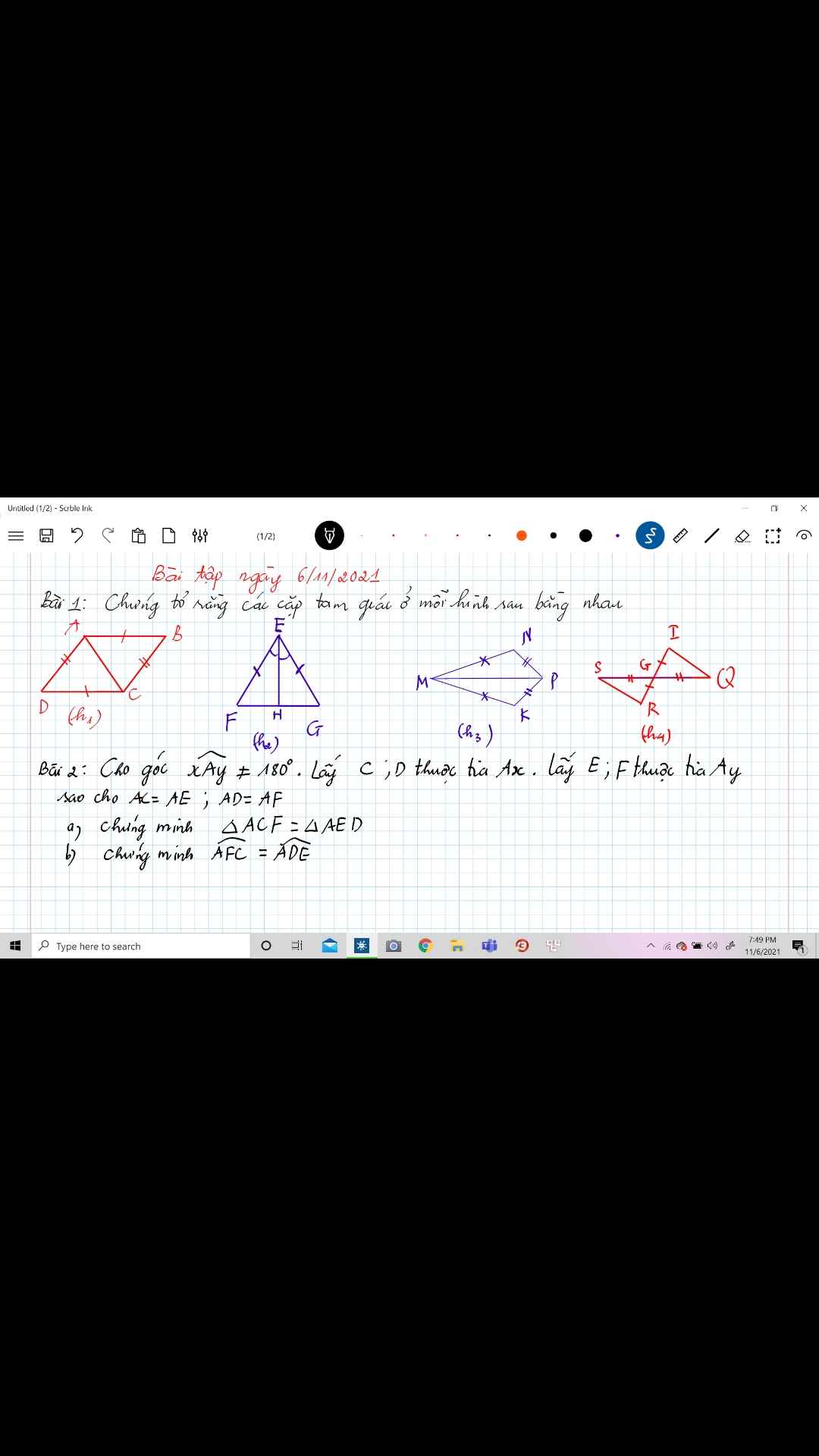
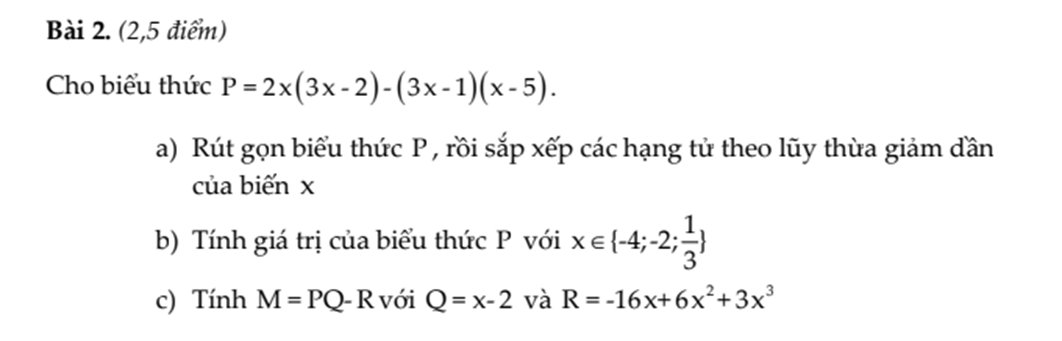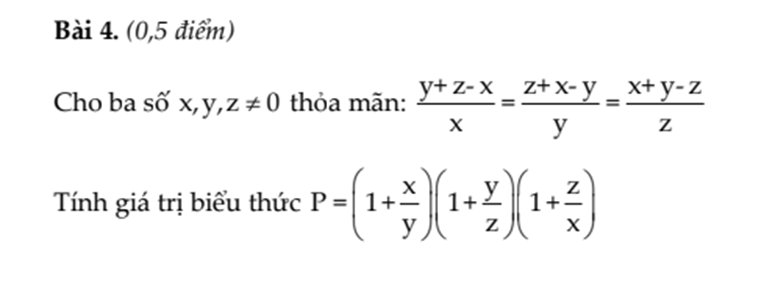Bài 2:
a: \(P=2x\left(3x-2\right)-\left(3x-1\right)\left(x-5\right)\)
\(=6x^2-4x-\left(3x^2-15x-x+5\right)\)
\(=6x^2-4x-3x^2+16x-5\)
\(=3x^2+12x-5\)
b: Thay x=-4 vào P, ta được:
\(P=3\cdot\left(-4\right)^2+12\cdot\left(-4\right)-5\)
=48-48-5
=-5
Thay x=-2 vào P, ta được:
\(P=3\cdot\left(-2\right)^2+12\cdot\left(-2\right)-5\)
=12-24-5
=-12-5=-17
Thay x=1/3 vào P, ta được:
\(P=3\cdot\left(\dfrac{1}{3}\right)^2+12\cdot\dfrac{1}{3}-5=\dfrac{1}{3}+4-5=\dfrac{1}{3}-1=-\dfrac{2}{3}\)
c: M=PQ-R
\(=\left(3x^2+12x-5\right)\cdot\left(x-2\right)-\left(3x^3+6x^2-16x\right)\)
\(=3x^3-6x^2+12x^2-24x-5x+10-3x^3-6x^2+16x\)
=-13x+10
B4:\(\dfrac{y+z-x}{x}\)=\(\dfrac{z+x-y}{y}\)=\(\dfrac{x+y-z}{z}\)
⇒\(\dfrac{y+z-x}{x}\)+2=\(\dfrac{z+x-y}{y}\)+2=\(\dfrac{x+y-z}{z}\)+2
⇒\(\dfrac{x+y+z}{x}\)=\(\dfrac{x+y+z}{y}\)=\(\dfrac{x+y+z}{z}\)
TH1:x+y+z=0
⇒x=-y-z
y=-z-x
z=-x-y
P=\(\left(1+\dfrac{-y-z}{y}\right)\).\(\left(1+\dfrac{-z-x}{z}\right)\).\(\left(1+\dfrac{-x-y}{x}\right)\)
=\(\dfrac{-z}{y}\).\(\dfrac{-x}{z}\).\(\dfrac{-y}{x}\)=-1
TH2:x=y=z
P=\(\left(1+\dfrac{x}{x}\right)\).\(\left(1+\dfrac{x}{x}\right)\).\(\left(1+\dfrac{x}{x}\right)\)=2.2.2=8
Phần TH2 bạn thay bằng biến y hay z cx đc nhé