Ta có: \(x^2-3x+2=\left(1-x\right)\sqrt{3x-2}\) \(\left(x\ge\dfrac{2}{3}\right)\)
\(\Leftrightarrow\left(x-1\right)\left(x-2\right)-\left(1-x\right)\sqrt{3x-2}=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-2+\sqrt{3x-2}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\x-2+\sqrt{3x-2}=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\left(TM\right)\\\sqrt{3x-2}=2-x\left(1\right)\end{matrix}\right.\)
Xét (1) ta có: \(\left\{{}\begin{matrix}2-x\ge0\\3x-2=4-4x+x^2\end{matrix}\right.\)\(\Leftrightarrow\)\(\left\{{}\begin{matrix}2\ge x\\x^2-7x+6=0\end{matrix}\right.\)\(\Leftrightarrow\)\(\left\{{}\begin{matrix}x\le2\\\left[{}\begin{matrix}x=6\left(KTM\right)\\x=1\left(TM\right)\end{matrix}\right.\end{matrix}\right.\)
Vậy nghiệm của phương trình là x=1
ĐKXĐ : x \(\ge\dfrac{2}{3}\)
Ta có \(\left(x-1\right)\left(x-2\right)=\sqrt{3x-2}\left(1-x\right)\)
<=> \(\left(x-1\right)\left(x-2+\sqrt{3x-2}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\\sqrt{3x-2}=2-x\end{matrix}\right.\)
Khi x - 1 = 0 <=> x = 1 (tm)
Khi \(\sqrt{3x-2}=2-x\)
<=> \(\left\{{}\begin{matrix}3x-2=x^2-4x+4\\\dfrac{2}{3}\le x\le2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x^2-7x+6=0\\\dfrac{2}{3}\le x\le2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(x-1\right)\left(x-6\right)=0\\\dfrac{2}{3}\le x\le2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x=1\\x=6\end{matrix}\right.\\\dfrac{2}{3}\le x\le2\end{matrix}\right.\Leftrightarrow x=1\)
Vậy phương trình 1 nghiêm \(x=1\)
\(ĐK:x\ge\dfrac{2}{3}\)
\(\Leftrightarrow\left(x-2\right)^2+x-2=\left(1-x\right)\sqrt{3x-2}\)
\(\Leftrightarrow\left(x-2\right)\left(x-2+1\right)=\left(1-x\right)\sqrt{3x-2}\)
\(\Leftrightarrow\left(x-2\right)\left(x-1\right)=\left(1-x\right)\sqrt{3x-2}\)
\(\Leftrightarrow x-2=-\sqrt{3x-2}\)
\(\Leftrightarrow2-x=\sqrt{3x-2}\)
\(\Leftrightarrow\left(2-x\right)^2=\left(\sqrt{3x-2}\right)^2\)
\(\Leftrightarrow4-4x+x^2=3x-2\)
\(\Leftrightarrow x^2-7x+6=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=6\end{matrix}\right.\) (vi-et )
Vậy S=\(\left(1;6\right)\)











 giúp mình câu 2 với ạaaaaa
giúp mình câu 2 với ạaaaaa


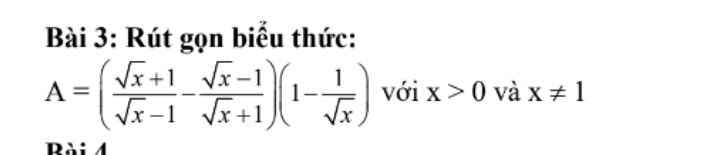








 Em cần giúp câu c và d ạ, mn giúp em với em đang cần gấp
Em cần giúp câu c và d ạ, mn giúp em với em đang cần gấp