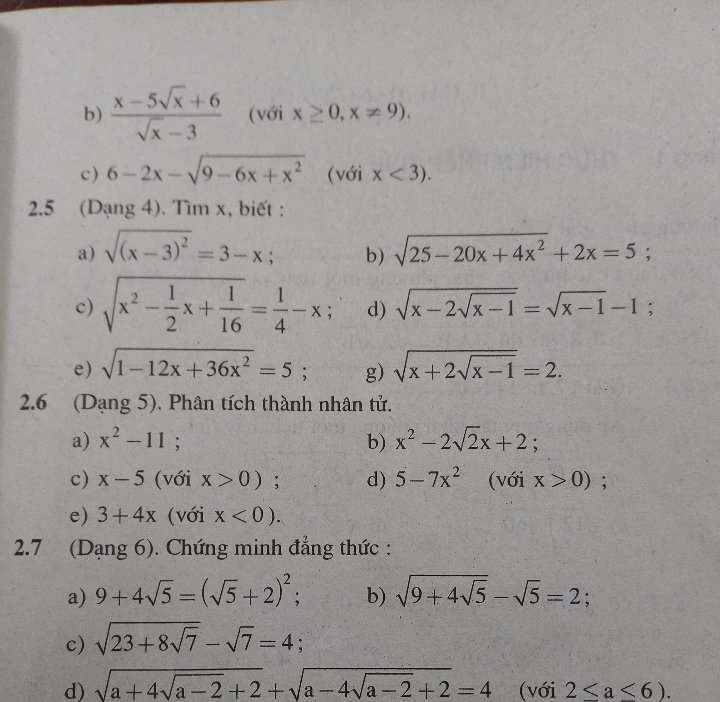2.7
a/ $9+4\sqrt{5}=2^2+2.2\sqrt{5}+(\sqrt{5})^2=(2+\sqrt{5})^2$
b/ $\sqrt{9+4\sqrt{5}}-\sqrt{5}=\sqrt{(2+\sqrt{5})^2}-\sqrt{5}$
$=|2+\sqrt{5}|-\sqrt{5}=2+\sqrt{5}-\sqrt{5}=2$
c/ $\sqrt{23+8\sqrt{7}}-\sqrt{7}=\sqrt{4^2+2.4\sqrt{7}+(\sqrt{7})^2}-\sqrt{7}=\sqrt{(4+\sqrt{7})^2}-\sqrt{7}$
$=4+\sqrt{7}-\sqrt{7}=4$
d.
$\sqrt{a+4\sqrt{a-2}+2}+\sqrt{a-4\sqrt{a-2}+2}$
$=\sqrt{(a-2)+2.2\sqrt{a-2}+2^2}+\sqrt{(a-2)-2.2\sqrt{a-2}+2^2}$
$=\sqrt{(\sqrt{a-2}+2)^2}+\sqrt{(\sqrt{a-2}-2)^2}$
$=|\sqrt{a-2}+2|+|\sqrt{a-2}-2|$
$=\sqrt{a-2}+2+2-\sqrt{a-2}=4$ (do $a\leq 6$ nên $\sqrt{a-2}-2\leq 0$ nên $|\sqrt{a-2}-2|=2-\sqrt{a-2}$)
2.5
a.
$\sqrt{(x-3)^2}=3-x$
$\Leftrightarrow |x-3|=3-x$
$\Leftrightarrow 3-x\geq 0$
$\Leftrightarrow x\leq 3$
b.
$\sqrt{25-20x+4x^2}+2x=5$
$\Leftrightarrow \sqrt{(2x-5)^2}=5-2x$
$\Leftrightarrow |2x-5|=5-2x$
$\Leftrightarrow 5-2x\geq 0$
$\Leftrightarrow x\leq \frac{2}{5}$
c.
$\sqrt{x^2-\frac{1}{2}x+\frac{1}{16}}=\frac{1}{4}-x$
$\Leftrightarrow \sqrt{(x-\frac{1}{4})^2}=\frac{1}{4}-x$
$\Leftrightarrow |x-\frac{1}{4}|=\frac{1}{4}-x$
$\Leftrightarrow \frac{1}{4}-x\geq 0$
$\Leftrightarrow x\leq \frac{1}{4}$
2.5
d. ĐKXĐ: $x\geq 1$
PT $\Leftrightarrow \sqrt{(\sqrt{x-1}-1)^2}=\sqrt{x-1}-1$
$\Leftrightarrow |\sqrt{x-1}-1|=\sqrt{x-1}-1$
$\Leftrightarrow \sqrt{x-1}-1\geq 0$
$\Leftrightarrow \sqrt{x-1}\geq 1$
$\Leftrightarrow x\geq 2$
Kết hợp đkxđ suy ra $x\geq 2$
e.
PT $\Leftrightarrow \sqrt{(6x-1)^2}=5$
$\Leftrightarrow |6x-1|=5$
$\Leftrightarrow 6x-1=\pm 5$
$\Leftrightarrow x=1$ hoặc $x=\frac{-2}{3}$
g.
ĐKXĐ: $x\geq 1$
PT $\Leftrightarrow \sqrt{(\sqrt{x-1}+1)^2}=2$
$\Leftrightarrow |\sqrt{x-1}+1|=2$
$\Leftrightarrow \sqrt{x-1}+1=2$
$\Leftrightarrow \sqrt{x-1}=1$
$\Leftrightarrow x-1=1$
$\Leftrightarrow x=2$ (tm)