Question

Giúp em câu c thôi ạ, em cảm ơn

Answer 1

Lời giải:

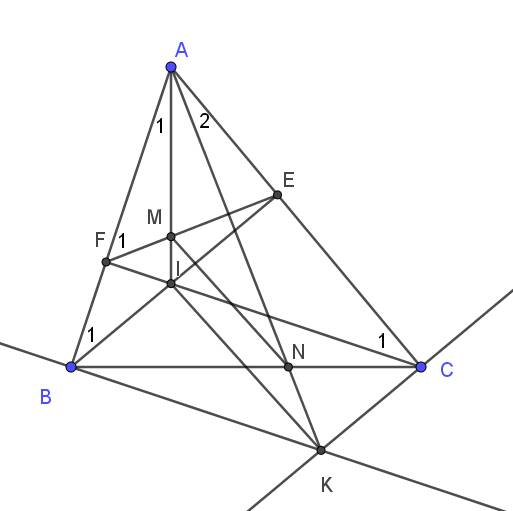
a. Xét tam giác $AEB$ và $AFC$ có:

$\widehat{A}$ chung

$\widehat{AEB}=\widehat{AFC}=90^0$

$\Rightarrow \triangle AEB\sim \triangle AFC$ (g.g)

b.

Từ tam giác đồng dạng phần a suy ra $\frac{AE}{AF}=\frac{AB}{AC}$

Xét tam giác $AEF$ và $ABC$ có:

$\widehat{A}$ chung

$\frac{AE}{AF}=\frac{AB}{AC}$ 

$\Rightarrow \triangle AEF\sim \triangle ABC$ (c.g.c)

$\Rightarrow \widehat{AFE}=\widehat{ACB}$

c. Từ kết quả phần a suy ra $\widehat{B_1}=\widehat{C_1}$
Xét tam giác $ABE$ và $ICE$ có:

$\widehat{B_1}=\widehat{C_1}$ (cmt)

$\widehat{AEB}=\widehat{IEC}=90^0$

$\Rightarrow \triangle ABE\sim \triangle ICE$ (g.g)

$\Rightarrow \frac{AB}{AE}=\frac{IC}{IE}=\frac{BK}{IE}$
Vì $BICK$ là hbh nên $BK\parallel CI, BI\parallel CK$. Mà $CI\perp AB, BI\perp AC$ nên $BK\perp AB, CK\perp AC$

$\Rightarrow \widehat{ABK}=\widehat{ACK}90^0$

Xét tam giác $ABK$ và $AEI$ có:

$\widehat{ABK}=\widehat{AEI}=90^0$
$\frac{AB}{AE}=\frac{BK}{EI}$

$\Rightarrow \triangle ABK\sim \triangle AEI$ (c.g.c)

$\Rightarrow \widehat{BAK}=\widehat{EAI}$

$\Rightarrow \widehat{A_1}=\widehat{A_2}$

Xét tam giác $FAI$ và $CAK$ có:

$\widehat{A_1}=\widehat{A_2}$
$\widehat{AFI}=\widehat{ACK}=90^0$

$\Rightarrow \triangle FAI\sim \triangle CAK$ (g.g)

$\Rightarrow \frac{FI}{FA}=\frac{CK}{CA}$

--------------

Từ kq phần b suy ra $\widehat{F_1}=\widehat{ACB}=\widehat{ACN}$
Xét tam giác $AFN$ và $ACN$ có:

$\widehat{A_1}=\widehat{A_2}$

$\widehat{F_1}=\widehat{ACN}$

$\Rightarrow \triangle AFM=\triangle ACN$ (g.g)

$\Rightarrow \frac{AM}{AN}=\frac{AF}{AC}$

Do $\triangle FAI\sim \triangle CAK$ (cmt)

$\Rightarrow \frac{AF}{AC}=\frac{AI}{AK}$

$\Rightarrow \frac{AM}{AN}=\frac{AI}{AK}$

$\Rightarrow MN\parallel IK$ (theo định lý Talet)

Answer 2

Hình vẽ

Answer 3

a: Xét ΔAEB vuông tại E và ΔAFC vuông tại F có

\(\widehat{EAB}\) chung

Do đó: ΔAEB~ΔAFC

b: Ta có: ΔAEB~ΔAFC

=>\(\dfrac{AE}{AF}=\dfrac{AB}{AC}\)

=>\(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)

Xet ΔAEF và ΔABC có

\(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)

\(\widehat{EAF}\) chung

Do đó: ΔAEF~ΔABC

c: Ta có: BICK là hình bình hành

=>BI//CK và BK//CI

Ta có: BI//CK

BI\(\perp\)AC

Do đó: CK\(\perp\)CA

Ta có: BK//CI

CI\(\perp\)AB

Do đó:BK\(\perp\)BA

Xét tứ giác ABKC có \(\widehat{ABK}+\widehat{ACK}=90^0+90^0=180^0\)

nên ABKC là tứ giác nội tiếp

=>\(\widehat{AKC}=\widehat{ABC}\)

mà \(\widehat{ABC}=90^0-\widehat{FAI}\) và \(\widehat{AKC}=90^0-\widehat{KAC}\)

nên \(\widehat{FAI}=\widehat{KAC}\)

Xét ΔAFI vuông tại F và ΔACK vuông tại C có

\(\widehat{FAI}=\widehat{CAK}\)

Do đó: ΔAFI~ΔACK

=>\(\dfrac{FI}{CK}=\dfrac{FA}{CA}\)

=>\(\dfrac{FI}{FA}=\dfrac{CK}{CA}\)