a: \(\dfrac{A}{B}=\dfrac{x^3+x+3x^2+3+2}{x^2+1}=x+3+\dfrac{2}{x^2+1}\)
\(a,A:B=\left(x^3+x+3x^2+3+2\right):\left(x^2+1\right)\\ =\left[x\left(x^2+1\right)+3\left(x^2+1\right)+2\right]:\left(x^2+1\right)\\ =x+3\left(\text{dư }2\right)\\ b,A:B=\left(x^4-2x^3+3x^2-2x^2+4x-6+9x-5\right):\left(x^2-2x+3\right)\\ =\left[x^2\left(x^2-2x+3\right)-2\left(x^2-2x+3\right)+9x-5\right]:\left(x^2-2x+3\right)\\ =x^2-2\left(\text{dư }9x-5\right)\)









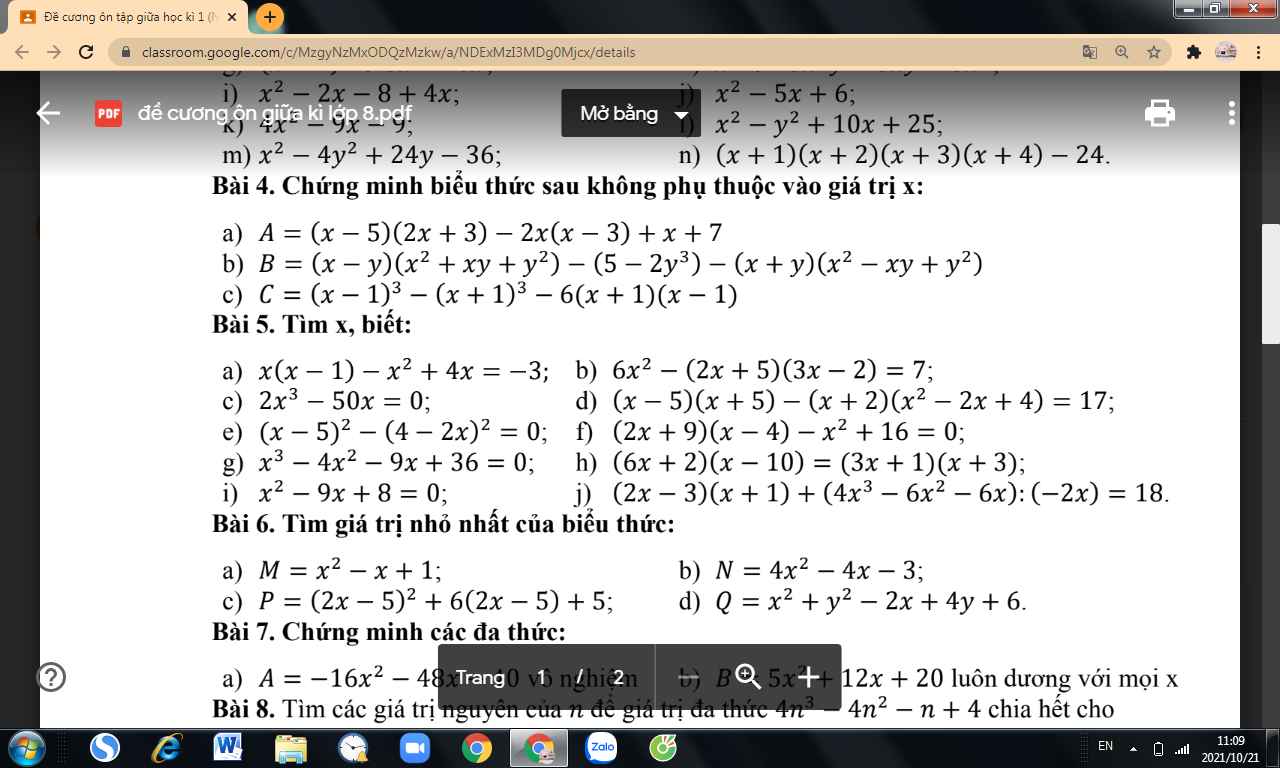
 mọi người giải giúp em bài này với ạ em đang cần gấp ạ
mọi người giải giúp em bài này với ạ em đang cần gấp ạ
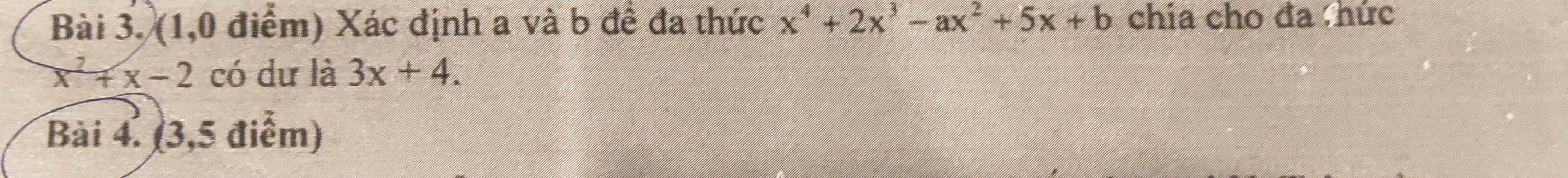 Mọi ng giúp em giải bài này với ạ, em cần gấp.
Mọi ng giúp em giải bài này với ạ, em cần gấp.
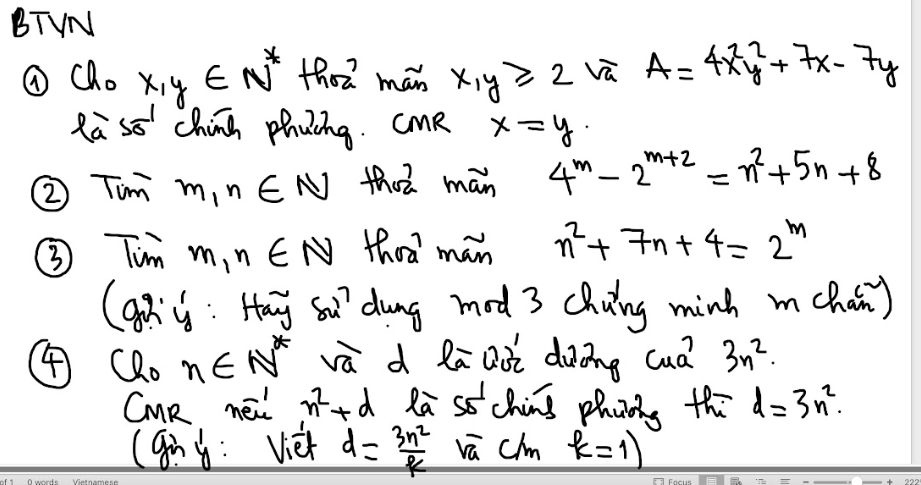





 em cần giải gấp bài 3 chi tiết mọi người giúp em với ạ. Làm bài dưới dạng phân số ạ em cần gấp
em cần giải gấp bài 3 chi tiết mọi người giúp em với ạ. Làm bài dưới dạng phân số ạ em cần gấp