Lời giải:
Để $x^4+2x^3-ax^2+5x+b$ chia $x^2+x-2$ dư $3x+4$ thì:
$x^4+2x^3-ax^2+5x+b=(x^2+x-2)Q(x)+3x+4$ với $Q(x)$ là đa thức thương.
$\Leftrightarrow x^4+2x^3-ax^2+5x+b=(x-1)(x+2)Q(x)+3x+4$
Cho $x=1$ thì:
$8-a+b=7\Leftrightarrow a-b=1(1)$
Cho $x=-2$ thì:
$-10-4a+b=-2\Leftrightarrow -4a+b=8(2)$
Từ $(1); (2)\Rightarrow a=-3; b=-4$

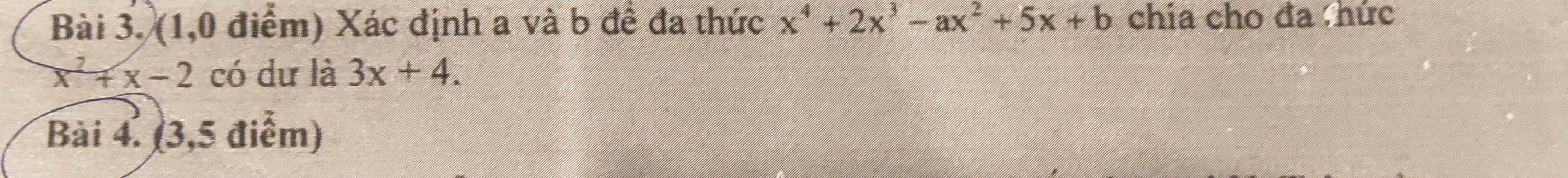 Mọi ng giúp em giải bài này với ạ, em cần gấp.
Mọi ng giúp em giải bài này với ạ, em cần gấp.


 mọi người giải giúp em bài này với ạ em đang cần gấp ạ
mọi người giải giúp em bài này với ạ em đang cần gấp ạ
 em cần giải gấp bài 3 chi tiết mọi người giúp em với ạ. Làm bài dưới dạng phân số ạ em cần gấp
em cần giải gấp bài 3 chi tiết mọi người giúp em với ạ. Làm bài dưới dạng phân số ạ em cần gấp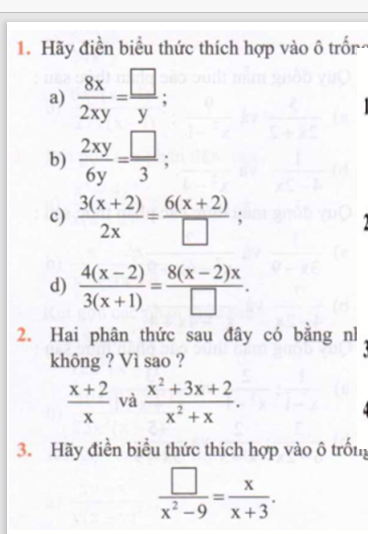 Mọi người giải giúp em với ạ em đang cần gấp ạ
Mọi người giải giúp em với ạ em đang cần gấp ạ











